You have 8 liters of water in a jug and you want to split it evenly into two lots of 4 liters.
You have 2 other water jugs which hold 3 and 5 liters each. None of the jugs have any markings.
How can you measure out 4 liters?
Follow these instructions:
- Fill the 5-liter jug from the 8-liter jug.
- Fill the 3-liter jug from the 5-liter jug.
- Pour the 3-liter jug in the 8-liter jug.
- Pour the 2 remaining liters from the 5-liter jug to the 3-liter jug.
- Fill the 5-liter jug from the 8 liter-jug.
- Fill the 3-liter jug from the 5-liter jug. Since only 1 more liter fits in the 3-liter jug, there will be 4 liters left in the 5-liter jug.
- Pour the 3-liter jug into the 8-liter jug.
Since we haven’t lost any water, there is now 4 liters in the 5-liter jug, and hence the other 4-liters in the 8-liter jug.
General case
You have two water jugs which each hold \(A\) and \(B\) liters of water respectively. Both \(A\) and \(B\) are integers and the water jugs have no markings. You can fill the jugs as much as you want from a tap.
What are the quantities can you measure out if both jugs start out empty?
You can measure out any multiple of \(\gcd(A, B)\).
Proof
First note that at the end of any action, both jugs can’t be partially full. There are no markings on the jugs, so we can only stop pouring when either the source is empty or the destination is full. Thus is it is never useful to empty a partially full jug - that would just leave us with the other jug completely full or empty which can be reached directly from the start.
This leaves the only useful actions as:
- Fill an empty jug
- Empty a full jug
- Pour a full jug into the other jug until either the other jug is full, or the first jug is empty
Let \(a\) and \(b\) be the current amounts of water in jug \(A\) and \(B\) respectively. If we plot the valid paths on a cartesian grid, then valid region that we can be within is along the perimeter where \(a=0\), \(a=A\), \(b=0\) or \(b=B\). This forms a rectangle.
Valid paths in this space will be:
- Horizontal lines between the top and bottom edges: Filling or emptying jug \(A\)
- Vertical lines between the left and right edges: Filling or emptying jug \(B\)
- Negative diagonal lines from one side to the another: Pouring one jug into the other.
Instead of the moving horizontally or vertically, we can instead imagine it continuing in a straight line into a copy of the rectangle. In this case, the real quantities will be given by \(a \mod A\) and \(b \mod B\) to bring as back into the original rectangle:
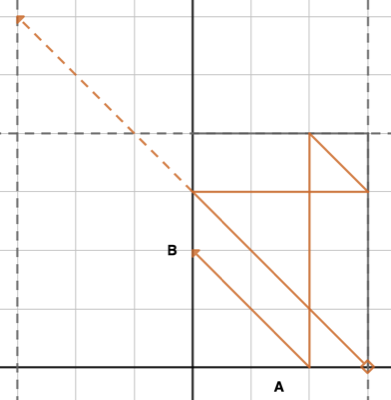
Since we start with empty jugs, all valid paths start at \((0, 0)\), hence all valid paths can be mapped to the negative diagonal line \(a = -b\).
The strategy
Traveling up along the negative diagonal corresponds to the following strategy:
- If \(A\) is empty, fill \(A\)
- If \(B\) is full, empty \(B\)
- Otherwise pour as much water as possible from \(A\) into \(B\).
- Stop when you have the required quantity.
Traveling down along the line simply swaps \(A\) and \(B\) in this strategy. This will reach all possible values.
Valid values
Suppose the final quantity is in jug \(B\). Then jug \(A\) is either full or empty and in either case \(a = 0 \mod A = x A\) for some integer \(x\). \(b\) can also be written as \(b' + y B\) for some integer \(y\). In combination with our path equation:
\[\begin{align} a = -b & = 0 \mod A \\ b & = x A \\ b' + (-y) B & = x A \\ b' & = x A + y B \end{align}\]By Bézout’s theorem the values of \(b'\) that satisfy this are the multiples of \(\gcd(A, B)\). By symmetry we get the same result if we want the final quantity to finish in jug \(A\).
If the desired quantity doesn’t fit in a single jug then we can first measure out and keep aside a multiple of either \(A\) or \(B\) and then follow the strategy above once the required value fits in a single jug.
More than 2 jugs
This extends to more than 2 jugs. See a discussion here.