There is a square plot of land with 1 km long sides. A perfectly straight powerline runs underneath through the plot, but we don’t know where it enters or exits.
You want to find any part of the powerline. You could dig around the entire perimeter (4 km), but that would be wasteful as you could get the same result by only digging up 3 sides of the square (3 km).
Can you do better?
We can trivially do better by cutting an X through the plot, cutting lines from opposite corners. This gives a length of \(2 \sqrt{2} \approx 2.83\) km.
We can do better by cutting two adjacent sides, then cutting a line from the opposite corner to the center. This gives a length of \(2 + \frac{\sqrt{2}}{2} \approx 2.71\) km.
We can improve this slightly by bringing in the two lines along the side until they meet at 120 degrees:
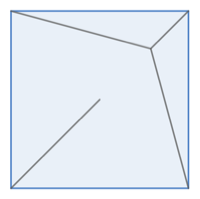
The short diagonal has a length of \(a = \frac{\sqrt{2}}{2}\). This gives a total length of \(2 \frac{2 a}{\sqrt{3}} + 2 a - \frac{a}{\sqrt{3}} \approx 2.64\) km.
(This may not be optimal.)