A fly is caught in a spider’s web and the spider is trying to catch it.

The fly and the spider start on the pictured intersections and take turns moving. During its turn the creature can move along an edge to a connected intersection - it must move, it can’t stay still.
How can the spider catch the fly if it has to move first?
Color the intersections as follows so that every move alternates between red and blue nodes, apart from the top node:
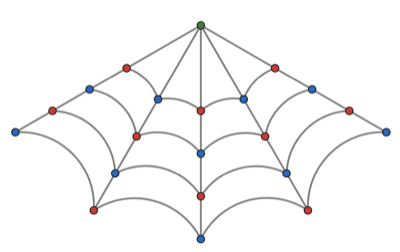
In the starting position, both the spider and the fly are on the same color. As long as the spider and fly stay on the red and blue nodes, they will always be on the same color after they both move. In this case the spider can’t catch the fly because the spider will always be forced to move to a node of the opposite color to the fly on its turn.
The only way to change this is to move up to the top green node. Once at the green node the spider can move so that it is on the same color as the fly after the spider’s move. The spider has changed the relative parity of their positions.
After this it can corner the fly by moving towards the fly’s position. The fly can’t get past the spider, because the spider controls of all the nodes around it. Since these controlled nodes are now the same color that the fly wants to move into, it controls the fly’s mobility.
Once in a corner, the fly has no choice but to move to a node where the spider can move to and catch it.
This is a type of Pursuit-evasion problem.