Four-card problem
4 playing cards are placed in front of you. Two are face-down, with one red back and one black back. Two are face-up, with one ace and one queen.

Which cards must you turn over to check that every ace has a black back?
You need to turn over the ace and the red-backed card:
- If the ace doesn’t have a black back, the rule is broken.
- If the red-backed card is an ace, the rule is also broken.
Note that both the face-down card with a black back and the queen can have anything on the other side without violating the rule.
Commentary
This is also known as the Wason selection task.
Five-card trick
A magician and their assistant perform a trick with a shuffled deck of cards. The assistant asks a member of the audience to draw 5 cards at random from the deck while the magician is blindfolded. The audience member hands the 5 cards to the assistant who examines the cards, hands one of them back to the audience member, arranges the remaining four cards and places them face down into a neatly stacked pile on a table.
The audience member is then allowed to move the pile on the table or change its orientation without disturbing the order of the cards in the pile. This is to ensure that the assistant can’t control the position of the pile.
The magician now removes their blindfold, examines the four cards on the table and determines the card held by the audience member from inspecting the four card pile.
Playing cards
How was this trick performed if the magician used an ordinary 52-card deck?
Out of the 5 drawn cards, the assistant chooses 2 cards which have the same suit.
Represent the value of the cards as their face value, with Ace=1, Jack=11, Queen=12, King=13.
Call the difference between the values of the two cards \(d\). Out of the two chosen cards, if the \(d > 6\) then select the highest value card; otherwise select the lowest value card.
Pass the selected card back to the audience. Put the other card down on the table - this will form the bottom of the pile for the magician.
Use the 3 remaining cards to encode a value, \(p\). If \(d \le 6\) then set \(p = d\), otherwise set \(p = 13 - d\). Place the 3 cards on the pile.
The magician can now look at the pile. From the bottom card in the pile the magician knows the suit of the selected card.
Let the value of the bottom card be \(v\). From looking at the order of the 3 top cards the magician can determine \(p\). If \(p + v < 13\) then the value of the selected card is \(p + v\) otherwise it is \(p + v - 13\).
Proof
It will always be the case there there are 2 cards of the same suit in the 5 drawn cards because there are only 4 suits (by the pigeon-hole principle).
Call the values of the 2 cards with the same suit \(v_1\) and \(v_2\) such that \(v_1 < v_2\). It is the case that either \(v_1 + p = v_2\) or \(v_2 + p \equiv v_1 \pmod{13}\) for some \(0 < p \le 6\).
If it was the case that \(v_1 + p = v_2 \text{ s.t. } 6 < p < 13\) then we could write it equivalently as \(v_1 + 13 - p \equiv v_2 \pmod{13} \text{ s.t. } 0 < 13 - p \le 6\).
Let \(d = v_2 - v_1\) (i.e. the difference between the values). If \(d \le 6\) then \(p = d\), otherwise \(p = 13 - d\) as in the description of the trick.
There are 6 possible values for \(p\): 1, 2, 3, 4, 5 and 6. We can encode \(3! = 6\) numbers by controlling the order of 3 cards. Thus we are able to encode \(p\) with the order of our three remaining cards.
Extended case
What is the maximum number of distinct cards the magician could perform this trick with?
The maximum size deck the trick can be performed with is 124.
In the general case the audience member draws \(n\) cards, we select one, and use the other \(n - 1\) cards to tell the magician the selected card. Here the maximum sized deck is \(n! + n - 1\) cards.
Algorithm
We will use the following definitions:
- Let the size of the deck be \(N = n! + n - 1\).
- Let the cards in the deck be represented by numbers from \(0\) to \(N - 1\).
- Let \(c_i\) be the values of the cards drawn by the audience member such that \(0 \le i < n \text{ and } c_i < c_{i+1}\).
- Let \(c_i^\prime\) be the values of the cards seen by the magician such that \(0 \le i < n - 1 \text{ and } c_i^\prime < c_{i+1}^\prime\).
- Let \(s = \left(\sum c_i\right) \mod n\).
- Let \(s^\prime = \left(\sum c_i^\prime\right) \mod n\).
- Let \(p = \left\lfloor \frac{c_s - s}{n} \right\rfloor\).
Choose \(c_s\) as the selected card.
Encode \(p\) as a permutation of the \(n - 1\) remaining cards, and set them in an pile.
The magician then looks at the pile and calculates \(p\) from the permutation of the cards in the pile and \(s^\prime\) from the sum of the cards in the pile. From that the magician calculates the value:
\[\chi = p n + (-s^\prime \mod n)\]The magician then can claim that \(c_s\) is the \(\chi\)th card which is not in the pile (not in \(c_i^\prime\)). Formally:
\[c_s = \chi + k \text{ where } c_{k-1}^\prime < \chi + k < c_{k}^\prime \text{ and } 0 \le k < n - 1 \label{card_trick:c_s_calc}\]Proof of correctness
We will split this proof into two parts. The first will prove that assistant will be able to follow the instructions, and the second part will prove that the magician can correctly guess the selected card.
Choosing \(c_s\) and \(p\)
There are at least \(n - s\) cards greater than or equal to \(c_s\): \(\{c_i \mid s \le i < n\}\).
There are at least \(s\) cards smaller than \(c_s\): \(\{c_i \mid 0 \le i < s\}\).
\[\begin{align} s \le & c_s \le N - (n - s) \\ s \le & c_s \le n! - 1 + s \\ 0 \le & c_s - s \le n! - 1 \\ \left\lfloor \frac{0}{n} \right\rfloor \le & \left\lfloor \frac{c_s - s}{n} \right\rfloor \le \left\lfloor \frac{n! - 1}{n} \right\rfloor \\ 0 \le & \left\lfloor \frac{c_s - s}{n} \right\rfloor < (n - 1)! \label{card_trick:bound} \end{align}\]We can now see from the definition of \(p\) that \(0 \le p < (n - 1)!\) and therefore \(p\) can be encoded as a permutation of \(n - 1\) cards. In addition, \(s\) is a number taken modulo \(n\) thus \(0 \le s < n\) and therefore it is always possible to select a card \(c_s\).
Determining \(c_s\)
Define \(q\) and \(r\) as follows:
\[c_s - s = q n + r \text{ s.t. } 0 \le r < n \label{card_trick:chi1def}\]Using the definition of \(s\) and \(s^\prime\):
\[\begin{align} c_s + s^\prime \equiv & s \pmod n \notag \\ c_s - s \equiv & -s^\prime \pmod n \notag \\ q n + r \equiv & -s^\prime \pmod n \notag \\ r \equiv & -s^\prime \pmod n \notag \\ r = & -s^\prime \mod n \text{ because } 0 \le r < n \end{align}\]Rearranging to solve for \(q\) we find that:
\[q = \frac{c_s - s - r}{n} = \left\lfloor \frac{c_s - s}{n} \right\rfloor = p\]Substituting our calculated values for \(q\), \(r\) and using the equation for \(\chi\):
\[\begin{align} c_s - s = & p n + (-s^\prime \mod n) = \chi \notag \\ c_s = & \chi + s \end{align}\]Given this it is sufficient to show that \(k = s\) is a unique solution to the equation for \(c_s\) used by the magician.
Let \(k = s + \Delta\):
\[\begin{align} & c_{s+\Delta-1}^\prime < \chi + s + \Delta < c_{s+\Delta}^\prime \\ \implies & c_{s+\Delta-1}^\prime < c_s + \Delta < c_{s+\Delta}^\prime \\ \implies & c_{s-1} < c_s < c_{s+1} & \text{ if } \Delta = 0 \\ c_{s+\Delta} < c_s + \Delta & \text{ if } \Delta > 0 \\ c_s + \Delta < c_{s+\Delta} & \text{ if } \Delta < 0 \\ & \text{ using } \notag \\ & c_i^\prime = c_i & \text{ where } i < s \\ c_{i+1} & \text{ where } i \ge s \\ & c_{i+j} \ge c_i + j \text{ where } 0 \le i+j < n \end{align}\]Only the \(\Delta = 0\) case is true and therefore \(k = s\) is the unique solution. Thus the magician correctly calculates \(c_s\).
Proof of optimality
The maximum number of different messages we can send the magician is limited by \(n!\). We have two choices:
- The card to select of which there are \(n\) options.
- The order of the remaining \(n - 1\) cards of which there are \((n - 1)!\) options (permutations).
This gives a total of \(n (n - 1)! = n!\) options. In addition, the magician will be able to see the \(n - 1\) cards in the pile.
This results in a upper-bound for the card deck of \(N = n! + n - 1\) cards.
Highest card
I challenge you to a game. I will deal four cards (from a regular 52 card deck), chosen randomly, face down. You get to look at #1 first and decide whether to keep it. If not, look at #2 and decide whether to keep that one. If not look at #3, and decide. If you don’t take that, then #4 is your choice.
If the value of your chosen card is \(n\), I will pay you $\(n\). I tell you that each game costs $10 to play, and we can play as many games as you like.
Note: The value of Jack, Queen and King are 11, 12 and 13 respectively. The value of the rest of the cards are their face value, with the Ace worth 1.
Can you come up with a strategy that will let you come out on top?
Use the following strategy:
- Keep the first card if it is 10 or greater, otherwise go to the second.
- Keep the second card if it is 9 or greater, otherwise go to the third.
- Keep the third card if it is 8 or greater, otherwise choose the fourth.
This will come out on ahead, on average.
Proof
Let us initially assume that there is an infinite deck for simplicity. There are an equal number of all face values, and now each card is independent of the previous ones.
For the 4th card the expected value is:
\[E_4 = \frac{1}{13} \sum_{i=1}^{13} i = 7\]For the 3rd card, if it is more than \(E_4\), we should keep it. Otherwise, look at the fourth. Thus the expected value is:
\[E_3 = \frac{1}{13} \sum_{i=8}^{13} i + \frac{1}{13} \sum_{i=1}^{7} E_4 = 8.615\]Likewise for the 2nd card, if it is more than \(E_3\), we should keep it. Otherwise, look at the third, giving the expected value is:
\[E_2 = \frac{1}{13} \sum_{i=9}^{13} i + \frac{1}{13} \sum_{i=1}^{8} E_3 = 9.533\]And finally, for the first card:
\[E_1 = \frac{1}{13} \sum_{i=10}^{13} i + \frac{1}{13} \sum_{i=1}^{9} E_2 = 10.138\]Thus our strategy gives us an expected value of $10.138 per game. Note that we assumed that there was an infinite number of cards. In reality, when a card is chosen, it wont appear again. Since we only reject low cards, this reduces our chances of getting more low cards. Thus our proof gives a lower bound on the expected value
This gives us an expected value of \(> $10\), letting you come out ahead.
In general, our strategy generalises to \(n\) initial cards with:
\[\begin{align} E_n & = 7 \\ E_{i-1} & = \frac{1}{13} \left( \lfloor E_i \rfloor E_i + \sum_{i=\lfloor E_i \rfloor + 1}^{13} i \right) \end{align}\]Pocket kings drawing dead
Tex is playing Texas Hold ‘Em, and was on an amazing winning streak. The gods of poker were chatting and came up with a diabolical plan to frustrate Tex.
“How about drawing dead before the flop?” asked the first god.
“Better yet, let’s give him pocket kings drawing dead!” replied the second.
“Brilliant,” exclaimed the first god, “But there are only six opponents, how can we do it?”
“Like this…”
Give a set of seven 2-card hands, including the pocket kings for Tex, such that Tex is drawing dead before the flop (he has zero chance of winning any portion of the pot).
The following hands result in Tex drawing dead:
| Tex | K\(\heartsuit\) K\(\diamondsuit\) |
| P1 | K\(\clubsuit\) A\(\diamondsuit\) |
| P2 | A\(\heartsuit\) K\(\spadesuit\) |
| P3 | A\(\clubsuit\) A\(\spadesuit\) |
| P4 | Q\(\heartsuit\) Q\(\diamondsuit\) |
| P5 | 7\(\heartsuit\) 7\(\diamondsuit\) |
| P6 | 7\(\clubsuit\) 7\(\spadesuit\) |
Proof
Tex can’t win on a pair because P3 already has a higher pair (pair of
As). In addition, no pair of As can come out on the board
because all As are accounted for.
Tex can’t win on a three-of-a-kind because all the other K are
accounted for. Three of any other card would result in a full house discussed
later.
Tex can’t win on a straight. If 2 to 6 comes up on the board,
P5 and P6 split the pot because they both will have 3 to 7
straights. If 8 to Q comes up on the board, P2 will win with a
10 to A straight. No other straights can come up on the board.
Tex can’t win on a flush. All the As are accounted for by other
players, so they will have a higher flush than anyone.
Tex can’t win on a full house. If three of some card come up on the board, P3
will win with a higher full house. Tex can’t get another K as they are
all accounted for.
Tex can’t win on a four-of-a-kind. If a four-of-a-kind comes up on the
board P1, P2 and P2 will split the pot because all have the highest kicker,
A. Tex can’t get four Ks as all the other Ks are
accounted for.
Second black ace
You have in front of you a shuffled deck of cards, face down. You get to choose a card from any position. Which card should you pick to maximize your chance of selecting the second black ace from the top.
Select the last (52nd) card.
Proof
Each position has an equal chance of being a black ace (since the deck is well shuffled). However, for all but the last card, some of the probability is that it is the first black ace. Thus the last card has the highest probability of being the second black ace.
Around the Earth
A rope with zero elasticity is placed tautly around the Earth’s equator.
Assume the Earth is a perfect sphere of radius 6378km.
Rope ring
How much longer would the rope need to be so that it can be form a ring 1m above the ground everywhere.
\(2 \pi \approx 6.28\) meters of rope is required.
Proof
Let \(c\) be the original length of rope, \(r\) the radius of the earth.
\[c = 2 \pi r\]Let \(\Delta c\) and \(\Delta r\) be the added rope and radius respectively.
\[\begin{align} c + \Delta c & = 2 \pi (r + \Delta r) \\ 2 \pi r + \Delta c & = 2 \pi r + 2 \pi \Delta r \\ \Delta c & = 2 \pi \Delta r \end{align}\]Thus the change in the length of rope is \(2 \pi \Delta r\) regardless of the original radius! In our problem \(\Delta r = 1\) m.
Pulled rope
Suppose instead we only want to pull the rope taut so that it was 1m high at one point. How much rope is required for this?
Adding 0.75 mm is sufficient to lift the rope up 1m!
Proof
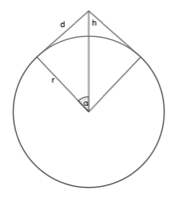
The length of the rope can be given by \(2 (\pi - \alpha) r + 2d\), thus the extra rope required is:
\(\Delta c = 2 (\pi - \alpha) r + 2d - 2 \pi r = 2 d - 2 \alpha r\) where \(\alpha = \arctan\left(\frac{d}{r}\right)\)
We can calculate \(d\) using Pythagoras’ forumla:
\[d^2 + r^2 = (r+h)^2\] \[d = \sqrt{2rh + h^2}\]Combining:
\[\Delta c = 2 \sqrt{2rh + h^2} - 2 r \arctan\left(\frac{\sqrt{2rh + h^2}}{r}\right)\]Using \(r = 6378 \text{ km}\) and \(h = 0.001 \text{ km}\):
\[\Delta c \approx 7.5 \times 10^{-7} \text{ km} = 0.75 \text{ mm}\]Belt loop
A thin belt is stretched around three pulleys, each of which is 1 m in diameter. The distances between the centers of the pulleys are 3 m, 4 m, and 6 m. How long is the belt?
The belt can be divided into straight and curved sections. The lengths of the straight sections are the same as the distances between the centers of the pulleys, and the curved sections total one complete circumference. So the total length is \(3 + 4 + 6 + \pi \approx 16.1\) m.
Buried powerline
There is a square plot of land with 1 km long sides. A perfectly straight powerline runs underneath through the plot, but we don’t know where it enters or exits.
You want to find any part of the powerline. You could dig around the entire perimeter (4 km), but that would be wasteful as you could get the same result by only digging up 3 sides of the square (3 km).
Can you do better?
We can trivially do better by cutting an X through the plot, cutting lines from opposite corners. This gives a length of \(2 \sqrt{2} \approx 2.83\) km.
We can do better by cutting two adjacent sides, then cutting a line from the opposite corner to the center. This gives a length of \(2 + \frac{\sqrt{2}}{2} \approx 2.71\) km.
We can improve this slightly by bringing in the two lines along the side until they meet at 120 degrees:
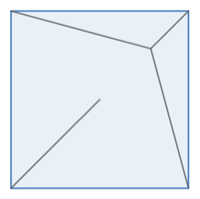
The short diagonal has a length of \(a = \frac{\sqrt{2}}{2}\). This gives a total length of \(2 \frac{2 a}{\sqrt{3}} + 2 a - \frac{a}{\sqrt{3}} \approx 2.64\) km.
(This may not be optimal.)
Cold walks
Which places on the earth can you walk one kilometer south, then one kilometer west, then one kilometer north and end up in the same spot?
Assume the earth is a perfect sphere and oceans or mountains don’t get in your way.
North pole
The simplest place with this property is the north pole. After you walk south, any amount of distance walking west will leave the north pole one kilometer north of you.
Other solutions
However, there are also an infinite number of places near the south pole with this property. Consider the circle centered on the south pole, with a circumference of one kilometer. Walking west for one kilometer from anywhere on this line will return you to the same position. Thus if we start one kilometer north of this circle, then we also satisfy the problem.
Walking once around the south pole is not the only way to stay in the same place. We could choose a smaller circle such that walking west one kilometer would circle the south pole \(n\) times, for any positive integer \(n\).
The circumference of a circle on a sphere is given by \(c = 2 \pi R \sin\left(\frac{r}{R}\right)\) where \(R\) is the radius of the sphere (the Earth). Since the circumference must be \(\frac{1}{n}\) we have:
\[r = R \arcsin\left(\frac{1}{2 \pi R n}\right)\]Since we need to start one kilometer north of any of these circles, that means that we need to start at any point:
\(\left(R \arcsin\left(\frac{1}{2 \pi R n}\right) + 1\right)\) kilometers north of the south pole for any positive integer \(n\).
Colored plane
Show that if each point in the plane is colored with 3 different colors, a unit segment must exist whose endpoints are the same color.
Set up two equilateral triangles ABC and BCD with unit sides which share a side. Let the color of A be green.
If B or C are green then we are done. Likewise if D is the same color as B or C.
This leaves the case where D is green. Since the triangle can be oriented in any direction, all points the same distance from A as D is colored green. This describes a green circle.
The circles has a larger than unit diameter, and thus there are an infinite number of points on the circle which are a unit distance from each other.
Finding the river
You are dropped on the surface of a very large planet, which has a single river which runs perfectly straight around the equator. You begin to explore the planet, in your dune buggy, by driving in a straight line away from the river, but a tornado hits you spinning you around and knocking you unconscious.
When you awake, you’ve forgotten which direction you had been travelling in. You do know however that you travelled 1000 km. You have an accurate compass and odometer on board. The river is in a canyon, and you can’t see it until you reach it.
You have enough fuel to go 6400 km. Can you make it back to the river (any point on the river)?
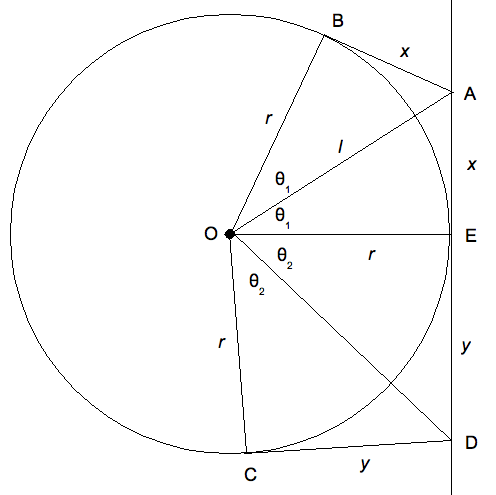
From point \(O\) travel:
- 1155 km to point \(A\)
- 577 km to point \(B\)
- 3665 km around the radius of the circle to point \(C\)
- 1000 km to point \(D\)
This will guarantee to come across the river.
Proof
Let the distance to the river be \(r\). The problem is equivalent to finding a curve that intersects with all of the tangents of a circle of radius \(r\).
To minimise the distance travelled we want to:
- Go directly to some tangent line (all are equivalent by symmetry)
- Follow it until we reach the circle
- Follow the circle around for some distance
- Then go to the closest point on our original tangent.
We will pick some arbitrary tangent, as all are equivalent. We choose the vertical tangent on the right side.
We need to head to some point \(A\) on the tangent, which we will say is an \(\theta_1\) from the horizontal. The length of the line from \(O\) to \(A\) is given by:
\[l = \frac{r}{\cos \theta_1}\]Next we travel from \(A\) to be \(B\), and this distance is given by:
\[x = r \tan \theta_1\]Next we travel around the circle from \(B\) to \(C\). This covers and angle of \(2 \pi - 2 \theta_1 - 2 \theta_2\). This gives adds a distance of:
\[a = 2 (\pi - \theta_1 - \theta_2) r\]Finally, to head from point \(C\) to point \(D\):
\[x = r \tan \theta_2\]This gives a total distance of:
\[\begin{align} d & = l + x + c + y \notag \\ & = r \left( \frac{1}{\cos \theta_1} + 2 (\pi - \theta_1 - \theta_2) + \tan \theta_1 + \tan \theta_2 \right) \end{align}\]We wish to minimise \(d\) thus we require that both of the following hold:
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = 0 \\ \frac{\partial d}{\partial \theta_2} & = 0 \end{align}\]Solving for \(\theta_1\):
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = r \left( \frac{\sin \theta_1}{\sin^2 \theta_1} - 2 + (1 + \tan^2 \theta_1) \right) \\ 0 & = \frac{\sin \theta_1}{\sin^2 \theta_1} + \tan^2 \theta_1 -1 \\ & = -\frac{2 \sin \theta_1-1}{\sin \theta_1-1} \\ & = 2 \sin \theta_1-1 \text{ where } \sin \theta_1 \ne 1 \\ \sin \theta_1 & = \frac{1}{2} \\ \theta_1 & = \frac{\pi}{6} \end{align}\]Solving for \(\theta_2\):
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = r \left(- 2 + (1 + \tan^2 \theta_2) \right) \\ 0 & = \tan^2 \theta_2 - 1 \\ \tan \theta_2 & = 1 \\ \theta_2 & = \frac{\pi}{4} \end{align}\]Substituting \(\theta_1\) and \(\theta_2\) into the equation for \(d\):
\[\begin{align} d & = r \left( \frac{2}{\sqrt{3}} + \frac{7 \pi}{6} + 1 + \frac{1}{\sqrt{3}} \right) \\ & = r \left( \sqrt{3} + 1 + \frac{7 \pi}{6} \right) \end{align}\]For our problem, \(r = 1000\) this gives a total distance of:
\[d \approx 6397 \text{ km}\]Ghost ships
Four ghost ships - \(A\), \(B\), \(C\) and \(D\) - sail on a night so foggy that visibility is nearly zero. All ships sail in a straight line, changing neither speed or heading. They have been sailing this way for a long time, and all have different headings.
Sometime in the night \(A\) collides with \(B\), but they pass through each other since they are ghost ships. However as they pass \(A\)’s captain hear \(B\)’s exclaim that it was their third collision that night.
Later in the night \(A\) run into \(C\) and hears the same exclamation from \(C\)’s captain.
Will \(A\) hit \(D\)?
\(A\) will definetly hit \(D\).
Proof
Plot the path of the ships in 3 dimensions, with time as the third dimension.
The paths of ships \(B\) and \(C\) form a plane (since they are different headings).
The path of \(A\) is on the same plane since it intersects with both \(B\) and \(C\). Likewise for \(D\). Hence the paths of \(A\) and \(D\) are co-planar.
\(A\) and \(D\) are on different headings, hence their paths intersect. They’ve both been sailing for a long time, hence their paths don’t intersect in the path, so they must intersect in the future.
Lake monster
You are in a row boat in the middle of a circular lake. On the shore of the lake is a monster who will eat you if it catches you. Luckily, the monster can’t swim and, on land, you can run faster than the monster. You are safe while you are in the boat, and if you reach the shore ahead of the monster then you can escape. Both you and the monster can turn instantaneously.
The monster can run 4 times as fast as you can row. How can you escape?
Let \(r\) be the radius of the lake.
First note that the simple strategy of rowing directly away from the monster fails. You need to travel a distance of \(r\), the monster needs to travel \(\pi r\) but does so 4 times faster.
However, you can travel further away from the center while keeping the monster on the opposite side. If you are closer than \(\frac{r}{4}\) from the center then you can row in a circle faster than the monster can circle the lake.
So first row to a distance of \(\frac{r}{4}\) from the center while keeping the monster opposite you. From there you can row directly to the closest shore. The monster will still have to travel a distance of \(\pi r\), but you only have to travel \(\frac{3}{4} r\).
Even though you are 4 times slower, you will reach the shore first because \(\pi r < 4 \times \frac{3}{4} r = 3 r\).
Extension
This strategy works as long as the monster is no more than \(\pi + 1 \approx 4.14\) times faster.
However, this strategy is not optimal and you can escape a monster who is up to ~4.6 times faster. For a proof see this blog post.
Planet shadow
A number of stationary perfectly-spherical planets of equal radius are floating in space. The surface of each planet includes a region that is invisible from the other planets. Show that the sum of these regions is equal to the surface area of one planet.
Fix any direction and call it “north.” Look at the north poles of all planets. A north pole is private if and only if there are no planets further to the north. Therefore, only the northernmost planet has a private north pole.
Since north was arbitrary, this is true for any direction. If we take the surface a single planet, every point on that planet corresponds to a direction. Thus each point on this surface maps to exactly one hidden point - the hidden point for that direction. Similarly, all hidden points map to a unique direction and thus a unique point on the surface of the planet.
Points and coins
I draw 10 points on a piece of paper. I give you 10 coins of the same size. Show that you can always cover all the points using the coins, without any coins overlapping.
First note that it is not true in general if we have \(n\) points and \(n\) coins. Any layout of coins will always have gaps, and will fail to cover a sufficiently dense set of points.
Instead consider a infinite hexagonal packing of circles. The density of such a packing is \(\frac{\pi}{2\sqrt{3}}\). Take a randomly translated close packing. Then:
\[\begin{align} P(\text{At least one point is not covered}) \le & \sum_{i=0}^{10} P(\text{The } i\text{th point is not covered}) \\ = & 10 \frac{\pi}{2\sqrt{3}} \\ \le & 9.069 \\ < & 1 \end{align}\]Note that this is true regardless of the covariance of the probabilities. Covariance can only lower the calculated probability.
Since there the probability is less than 1, there is some probability that a random translation of the hexagonal packing will cover all the points. If there were no valid translations, then the probability would be 0, thus a convering translation must exist.
Finally, we note that at most 10 of the coins in the infinite packing must be covering points because each point can only be under at most one coin. Thus we only need to use 10 coins.
Worm and the apple
There is an apple with radius 31 mm. It is in the shape of a perfect sphere. A worm gets into the apple and eats a tunnel of total length 61 mm, and then leaves the apple. (The tunnel need not be a straight line.)
Prove that you can cut the apple with a straight slice through the center so that one of the two halves is not eaten.
First consider the problem for a circle instead of a ball.
Let \(A\) and \(C\) be the entry and exit points of the worm. Let \(B\) be the point opposite the worm’s entry point.

Note that the worm can never travel from \(A\) to be \(B\) as the distance is 62 mm.
Draw a line that bisects \(C\) and \(B\) and goes through the circle’s center (hence cuts the circle in two). By construction, all points on the line are equally far from \(C\) and \(B\). Thus if the tunnel touches the line, then it could also have reached \(B\). Since a tunnel between \(A\) and \(B\) is impossible, the tunnel cannot touch the line.
Cutting the apple along the line leaves the tunnel completely on one side, leaving the other side untouched by the worm.
For a sphere, replace the bisecting line with a bisecting plane where all points on the plane are eqi-distant from the points \(B\) and \(C\). The rest of the proof carries through.
10 wires
10 wires run underground between two buildings. Unfortunately, they are unlabelled so you don’t know which ends match up. You need to label the wires for the wires to be useful.
You only have a battery and lightbulb as equipment.
How many trips do you need to make between the two buildings to label all the wires?
You only need to make one round trip.
Proof
Starting in the first building number:
- Label 1 wire with \(A\).
- Connect the next 2 wires and label them with \(B\).
- Connect the next 3 wires and label them with \(C\).
- Connect the remaining 4 wires and label them with \(D\).
This accounts for all the wires as \(1+2+3+4 = 10\).
Now go to the second building. Using the battery and lightbulb, test every pair of wire against the others (45 tests) to check if they are connected.
Label the wire that is not connected to any other wire as \(A\), the wires that are only connected to each other as \(B\), the group of 3 connected wires as \(C\), and the group of 4 connected wires as \(D\).
Update the labels as follows:
- Take one wire from each group and connect them together. Append \(A\) to their labels - this will result in labels \(AA\), \(BA\), \(CA\) and \(DA\).
- Take another wire from each group (which has not yet been updated) and connect them together. Append \(B\) to the label. Only 3 of the groups will have a spare wire for this.
- Continue in this way connecting wires, appending \(C\) and \(D\) in turn. Each will have one less group with spare wires to update.
As before this accounts for all the wires as \(1+2+3+4 = 10\). Each wire now has a unique 2 letter label, because each wire in a given group got a different letter appended.
Now return to the first building. Disconnect the original connections. Using the battery and lightbulb, test every pair of wire against the others (45 tests) to check if they are connected.
Append \(D\) to the wire that is not connected to any other wire, \(C\) to the wires that are only connected to each other, \(B\) to the group of 3 connected wires, and \(A\) to the group of 4 connected wires.
The labels of the wires in the two building should now match, with each wire having a unique 2 letter label.
This strategy works for any triangular number numbers of wires.
3 prisoners in a line
3 prisoners are brought to a room with 3 red hats and 2 blue hats. They are told to line up single file facing forward, so that each prisoner can only see those in front of them. They are blindfolded and a hat is placed on each prisoners head. The remaining hats are disposed of.
The blindfolds are removed and the prisoners are told that the first person to correctly call out the colour of their hat will go free. They have one minute.
For a while the prisoners stand silent, but just before the minute is over the prisoner at the front correctly names the colour of their hat.
What was the colour of the hat on the prisoner at the front?
The prisoner at the front had a red hat.
Proof
The prisoner at the back can see the colours of the other two prisoners. If the hats were both blue then the prisoner could deduce that their own colour was red, and they would instantly say this. Since the prisoner at the back remained quiet we (and the two prisoners in front) know that least one of the front two prisoners has a red hat.
The middle prisoner can only see the colour of the front prisoner’s hat. If it was blue then the prisoner could deduce that their own hat colour was red. However, they do not speak. This means that the colour of the hat on the front prisoner must be red.
3 switches and a lightblub
You are in a room with 3 switches. One of the switches controls a lamp with an incandescent lightbulb in a nearby room. You may flip the switches as many times as you like. You may only enter the room with the lamp once. You cannot see if the lamp is on from the room with the switches.
How can you determine which switch controls the lamp?
Number the switches #1, #2 and #3. Use the following strategy:
- Turn on switch #1.
- Wait a suitably long time (we will arbitrarily choose one hour).
- Turn off switch #1.
- Turn on switch #2.
- Enter the room with the lamp.
-
Examine the lamp:
- If the lamp is on, switch #2 controls the lamp.
- If the lamp is off, but the lightbulb is warm to the touch, switch #1 controls the lamp.
- Otherwise switch #3 controls the lamp.
Attacking knights
What is the maximum number of knights which can be placed on a chess board with none of the knights attacking each other.
32 knights:

All the knights are on black squares, and knights on black squares can only attack white squares.
Proof
Pair up squares as in the following diagram. Paired squares are identified by the same piece.
A knight can only be placed on one of each pair of squares. Since this arrangement can be tiled across the entire chessboard, the knights can take up at most half the chess board: 32 squares.

Calendar cubes
Number the faces of two cubes so that they can always be placed side-by-side to show the current day of the month.
We need to be able to represent all numbers for 01 to 31.
0, 1 and 2 need to be paired with every number hence need to be on both cubes. The remaining numbers don’t need to be paired with each other, thus can be placed on either of the cubes.
This leaves us 6 remaining faces, but we have 7 remaining numbers. We can take advantage of the fact that the same face can represent both 6 and 9 by placing the face upside down.
Thus the following layout works:
- Cube 1: 0, 1, 2, 3, 4, 5
- Cube 2: 0, 1, 2, 6/9, 7, 8
Covering queens
Place 5 queens on a chessboard so that they attack every square.
There are several possible solutions. Here is one:
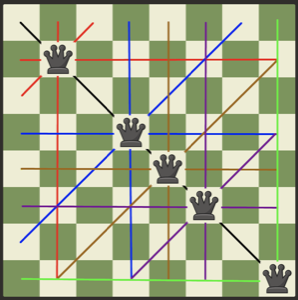
Note: A 4-queens solution is not possible, but the proof requires brute-force.
Dice groups
On a table in front of you there are two groups of 5 dice each. One of the groups adds to 12 and the other to 16. You are blindfolded and asked to create two piles which add up to the same number.
How can you do it?
Move a die from one pile to the other, so you have a pile of 6 dice and a pile of 4 dice. Flip all the dice in the pile of 4. The two piles will have the same sum.
Proof
First note that opposite sides of a dice add up to 7. Thus flipping the dice changes the value from \(x\) to \(7-x\). Filling a group of \(n\) dice changes the total from \(x\) to \(7n-x\).
The sum of the all the dice in front of you is 28. Thus if the total of one group is \(x\) then the total of the other group would be \(28-x\). If a group only had 4 dice then we could make the groups equal by flipping the 4 dice. The flipped group would have a total of \(7\times4-(28-x) = x\).
If we shift a die from one group to the other the overall total remains 28, but now we have a group of 4 which we can flip.
Flipping coins
On a table in front of you there are 100 coins, 20 heads up and 80 tails up. You are blindfolded and asked to create two groups of coins each with an equal number of heads up.
How can you do it?
Arbitrarily split the coins up into a group of 20 and a group of 80. Now flip all the coins in the group of 20. Now both groups have the same number of heads up.
Proof
Let the number of coins in the group of 80 be \(h_{80}\).
There are 20 coins with heads up initially, so immediately after we split up the groups, the number of heads in the group of 20 is \(20 - h_{80}\).
When we flip the coins in the group of 20, the number of heads in the group becomes \(20 - (20 - h_{80}) = h_{80}\). Thus now the two groups have the same number of heads showing.
Gold chain
You want to stay at an inn for seven nights. You only have a gold chain with seven links. The innkeeper agrees to accept this in payment for the stay, but you only want to pay for one night at a time.
You start to cut a link, but the innkeeper wants you to minimize the damage to the chain. What is the minimum number of cuts you must make, provided the provided the innkeeper is happy to return previously given links as change?
This is possible in one cut.
Cut a single link, the third one, dividing the chain into lengths of 1, 2, and 4. Then follow this day-by-day plan:
- Give 1 link.
- Give 2 links, get 1 link as change.
- Give 1 link.
- Give 4 links, get 3 links as change.
- Give 1 link.
- Give 2 links, get 1 link as change.
- Give 1 link.
This is equivalent to counting in binary.
Handshakes
A man and his wife are at a party. In the party there are 4 other couples for a total of 5 couples. During the party some people shake hands, however no one shakes hands with their spouse, and no one shakes hands with themselves.
At the end of the party the man asked all the other guests at the party (including his wife) how many different people they shook hands with. Each person tells him a different answer.
How many people did the man shake hands with?
The man shook hands with 4 people.
Proof
Let us label each person with the number of people they have shaken.
Everyone has shaken hands with at most 8 people, since there are only 8 people at the party besides that person and their spouse. So for every number between 1 and 8, there is a person who has shaken that many hands.
#8 must have shaken hands with everyone else other than their spouse. Thus the spouse must be #0, since everyone else has shaken at least one hand (#8’s). By the same logic, since all of the remaining people have shaken hands with #8, and none with #0, #7 must be married to #1. Likewise, #6 is married to #2 and #5 is married to #3.
The only people left are #4 and the man. Thus the man must be married to #4. Thus the man must have shaken hands with #8, #7, #6 and #5, but not #0, #1, #2, #3 or his wife #4. This gives 4 handshakes.
Jewel thieves
Two thieves conspire to steal a valuable necklace made of diamonds and rubies. The jewels are evenly spaced, but the diamonds and rubies are arbitrarily arranged. After they take it home, they decide that the only way to divide the jewels fairly is to physically cut the necklace in half.
Prove that, if there is an even number of diamonds and an even number of rubies, it’s possible to cut the necklace into two pieces, each of which contains half the diamonds and half the rubies.
Note that the necklace must be divided at two opposite points, as each thief will have to end up with the same number of jewels.
Start with arbitrary provisional cutting points which divide the necklace in two. If one side has more diamonds than the other, you rotate the cut by one jewel. If the switched jewels were the same, it changes nothing and you rotate again. If they’re different, the number of diamonds on one side will either go up one or down one. Eventually, by the time you’ve rotated the cut 180 degrees, the sides of the original cut will have swapped.
Since each rotation changes the number by one, and the diffence in the number of diamonds has been negated, then at some point they must have been equal. If the diamonds are equal then the rubies are also equal since each half has the same number of jewels.
Mislabelled marble cans
You have 3 cans. On is labelled “black” and contains only, one is labelled “white” and contains only white marbles, the last is labelled “mixed” and contains both black and white marbles.
All labels switched
Unfortunately, all the labels get switched so that none of the cans have their original label. How many marbles do you have to draw to determine which can is which?
You only need to draw one marble.
Proof
Draw a marble from the can labelled “mixed”.
If you draw a black marble it must be the “black” can since it cannot actually be the “mixed” can. Thus the can currently labelled “black” is the white can, since it cannot be either the “black” or “mixed” cans. Finally the can labelled “white” must be the mixed can.
Similarly if a white marble is drawn, the can labelled “mixed” is really “white”, the can labelled “white” is really “black” and the can labelled “black” is really “mixed”.
Two labels switched
What if only two of the labels were switched and one remained the same? How many marbles do you need to draw now?
You need to draw two marbles.
Proof
First note that one marble is not sufficient since there are 3 possible swaps. Single marble can only distinguish between two possibilities.
Start by drawing a marble from the can labelled “mixed”.
If a white marble draw a marble from the can labelled “black”. If this second marble is white, then the “mixed” can is correct, and the “black” label was swapped with the “white” label. If the second marble is black then the “black” can is correct and the “mixed” was swapped with the “white”.
If the first marble drawn was black then follow the above analysis with black and white reversed.
Marked prisoners
A group of 200 perfect logicians are taken prisoner. Each has either an
X or an O marked on their forehead. They can all see each
other, and the marks on the others’ foreheads. They have no way of seeing
the mark on their own forehead. They are no allowed any communication between
each other at all, on pain of death.
It happens that 100 of the prisoners have the X mark and the other 100
have the O mark. However, none of them know exactly how many people
have the X mark and how many people have the O mark.
Each night, at midnight, any prisoner who can correctly determine the mark
on their forehead may leave. They know their marks are either X or
O.
One day a guard being careless and was accidentally heard saying:
“I can see someone with an X mark on their forehead”
He is quickly disciplined, but everyone heard what he said.
Who leaves the prison, and on what night?
On the 100th day, all 100 prisoners with an X mark will leave. On
the day after 101st day, the 100 remaining prisoners with the O mark
will leave.
Proof
In the case of one prisoner with the X mark, he looks around and sees
that no one else has an X. Thus he is the only one the guard could
be referring to. Thus we have:
Theorem 1: If there is only one prisoner with an
Xmark, he leaves on the first night.
Let us set up the hypothesis that:
Hypothesis 1: If there are \(n\) prisoners with the
Xmark, nothing will happen for the first \((n-1)\) nights, then they will all leave on the \(n\)th night.
If there are \((n+1)\) prisoners with the X mark, then they all see \(n\)
other prisoners with the X mark. Thus they can all deduce that there
must be either \(n\) or \((n+1)\) prisoners with the X mark.
If we assume Hypothesis 1, then on the first \(n\) nights nothing will
happen. After the \(n\)th night they will be determine that there can not be
exactly \(n\) prisoners with the X mark. Hence they can all deduce that
they each have an X mark and they will all leave on the next night,
the \((n+1)\)th night. Thus we have:
Theorem 2: If Hypothesis 1 is true for a given \(n\) then it is also true for the case \((n+1)\).
We can see that Hypothesis 1 is true for the case \(n = 1\) by Theorem 1. Then using induction with Theorem 2 we can see that Hypothesis 1 is true for all \(n \ge 1\).
In our problem, we have the case where \(n = 100\) thus all the prisoners
with the X mark will leave on the 100th day. The prisoners with the
O mark will see them leave and can deduce that they do not have an
X. Since O is the only other option they will leave on the
next day, the 101st day.
Extra Consideration
What is the piece of information that the guard provides that each prisoner did not already know?
Each prisoner already knew that there was at least one X marked
prisoner. They also all knew they everyone else knew, and they everyone knew
that everyone knew. However this does not continue indefinitely.
In our problem, everyone knew that there were at least 99 X marked
prisoners. But when we get to meta-knowledge, we can only say that everyone
knew that everyone knew that there are at least 98 X marked
prisoners. Continuing further, our strongest statement of meta-meta-knowledge
is that, everyone knew that everyone knew that everyone knew that there are at
least 97 X marked prisoners.
This continues until we can’t say anything about the number X marked
prisoners.
When the informer speaks, the fact that there is at least 1 X marked
prisoner becomes common knowledge. Importantly, now everyone knows that
everyone knows that there is at least X marked prisoner. And everyone
knows that everyone knows that everyone knows… and so on indefinitely.
Sufficiently deep in this meta-knowledge, this adds new information. This is known as Common knowledge.
Made famous as xkcd’s Blue Eyes puzzle (solution).
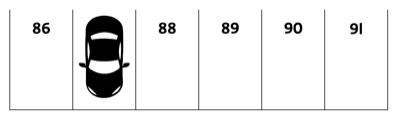
⇪Parking lot
What is the number of the parking space that the car is occupying?

The car in space 87.
This becomes more obvious if we turn the image upside down. The lots are actually numbered from 86-91:
Party hats
There is a party of logicians, and just towards the end of the party the host seats everyone down in a circle. They puts a hat on each person’s head such that everyone else could see it but the person themselves could not.
There were many, many different colours of hats. The host instructed them that a bell would be rung at regular intervals: at the moment when a person knew the colour of their own hat, they must leave at the next bell.
As they were all very good logicians, leaving at the wrong bell was unacceptable and would be disastrous to their reputations. The host reassures the group by stating that the puzzle would not be impossible for anybody present.
How did they all leave?
First we determine that there must be at least 2 of each hat colour. If there was a person with a unique hat colour, then they could in no way determine that their was even a valid colour. However, the host said that everyone has enough information to solve the puzzle and leave. Thus there must be at least two people with each hat colour.
We now form a hypothesis and prove it via induction:
Hypothesis: If there are \(n\) people with a hat of colour \(c\), then they will all leave on the \((n-1)\)th bell.
If there are only two people for a given colour \(c\), then both of them will count only one hat of colour \(c\) in the group. Thus they will both know that their own hat colour must also be \(c\). Therefore they both leave on the first bell, satisfying the Hypothesis.
Suppose there are \(n\) people with hats of a given colour \(c\), and suppose the Hypothesis is true for \(n-1\). Then everyone with hat colour \(c\) will see \(n-1\) people with colour \(c\). On the \((n-1)\)th bell none of them will leave, thus they will all conclude there must be more than \(n-1\) people with a hat of colour \(c\). Thus they will determine that they must have a hat of colour \(c\).
Therefore, because the Hypothesis is true for \(n=2\), and the Hypothesis being true for \(n-1\) implies it is true for \(n\), we have that the Hypothesis is true for all \(n \ge 2\).
Therefore, everyone eventually leaves. (Compare this with Marked prisoners).
Sorting hats
A group of prisoners are offered a chance of freedom. The prisoners will be brought in one at a time, and a black or white hat will be placed on their heads as they come in.
The prisoners must form a line with white hats on one side and black hats on the other. The prisoners can’t communicate, and can only choose their position in the line.
How can the prisoners succeed?
As each prisoner enters, they simply join the line at the point between an adjacent black and white hat. If there are only hats of one color they can join at either end of the line.
This always preserves the property that the line is always valid at all times. Note, that the prisoners don’t need to communicate beforehand.
Spinning room
You are trapped in a small square room. In the middle of each side of the room there is a hole. In each hole there is a push button that can be in either an off or on setting. You can’t see in the holes but you can reach your hands in them and push the buttons. You can’t tell by feel whether they are in the on or off position.
You may stick your hands in any two holes at the same time and push either, or both of the buttons as you please. Nothing will happen until you remove both hands from the holes. You succeed if you get all the buttons into the same position, after which time you will immediately be released from the room.
Unless you escape, after removing your hands the room will spin around, disorienting you so you can’t tell which side is which.
How can you escape?
Do the following in order until you escape:
- Push buttons on two opposite walls.
- Push buttons on two adjacent walls.
- Push buttons on two opposite walls.
- Push any one button.
- Push buttons on two opposite walls.
- Push buttons on two adjacent walls.
- Push buttons on two opposite walls.
You should be free by the end of the last instruction at latest.
Proof
Let us label all the states we could be in:
- \(A\): Two buttons ON, on opposite sides.
- \(B\): Two buttons ON, on adjacent sides.
- \(C\): Three buttons in the same state, and other other different.
If we push two opposite buttons, then if we are in state \(A\), then we go free. The other states remain the same. Thus first we carry this out, and if we are still in the room, we must be in state \(B\) or \(C\).
Now, if we are in state \(B\) and we push two adjacent buttons, then we either go free or go to state \(A\). But from above we know how to escape from state \(A\). Thus we push two adjacent buttons, then two opposite buttons. If we are still in the room, the starting position must have been state \(C\).
Note that up to this point we have been pushing two buttons at a time, so this always leaves state \(C\) the in state \(C\).
Now we know that we are in state \(C\). Pushing any one button will convert the state to either \(A\) or \(B\). But we know how to escape for \(A\) or \(B\), so we just repeat the procedure above.
In summary the possible states we are in after each step are:
\(\{A,B,C\}\) \(\xrightarrow{1} \{B,C\}\) \(\xrightarrow{2} \{A,C\}\) \(\xrightarrow{3} \{C\}\) \(\xrightarrow{4} \{A,B\}\) \(\xrightarrow{5} \{B\}\) \(\xrightarrow{6} \{A\}\) \(\xrightarrow{7} \{\}\)
Short and tall
Two hundred students are arranged in 10 rows of 20 children. The shortest student in each column is identified, and the tallest of these is marked \(A\). The tallest student in each row is identified, and the shortest of these is marked \(B\).
If \(A\) and \(B\) are different people, who is taller?
\(B\) is taller.
Proof
There are three different cases:
-
If \(A\) and \(B\) stand in the same row, then \(B\) is taller, since we know that \(B\) is the tallest student in their row.
-
If \(A\) and \(B\) stand in the same column, then again \(B\) is taller, since we know that \(A\) is the shortest student in their column.
-
If \(A\) and \(B\) share neither a row nor a column, then let \(C\) be the student who’s in the same column as \(A\) and the same row as \(B\). Then \(C\) is shorter than \(B\) (who is the tallest in their row) and taller than \(A\) (who is the shortest in their column), so \(B > C > A\).
In every case, \(B\) is taller than \(A\).
The bookworm
A 5 volume set of book sit on a shelf, in order. Each volume is 1 inch thick.
A bookworm eats its way from the front cover of the first volume to the back cover of the last volume. How far did the bookworm travel?
3 inches.
Proof
The front of volume 1 is directly next to volume 2 when arranged on the shelf. Likewise, the back of volume 5 is next to volume 4.
Thus the bookworm does not eat through volume 1 and 5, only 2, 3 and 4. It travels 3 books, thus 3 inches.
Birthday problem
How big does a group of people need to be before there is at least a 50% chance that two people share a birthday.
23 people.
Proof
For simplicity, ignore leap years. This won’t significantly affect the result.
Assume that all birthdays are equally likely. If birthdays are unequally distributed, then it only makes it more likely that people share a birthday.
We will determine the probability that no one shares a birthday with anyone. Adding people one at a time:
- The first person won’t share a birthday (as they are the only person). i.e. they have a \(1 = \frac{365}{365}\) chance of being unique.
- The second person only has to avoid the first person’s birthday for a \(\frac{364}{365}\) chance of being unique.
- The \(n\)th person has to avoid \(365-(n-1)\) days for a \(\frac{366-n}{365}\) chance of being unique.
Then the probability \(P'(n)\) that no one shares a birthday is the product that each individual has a unique birthday:
\[P'(n) = \frac{365 \times 364 \times ... \times (366-n)}{365^n} = \frac{365!}{(365-n)! 365^n}\]The probability that there are two people who share a birthday \(P(n)\) is the complement:
\[P(n) = 1 - \frac{365!}{(365-n)! 365^n}\]23 is the smallest number for which \(P(n) > 0.5\).
Other values
By the pigeonhole principle, you need 366 people to be guaranteed to be two people who share a birthday (367 to include leap years).
However chance climbs very quickly to be close to 1 with much smaller groups:
| n | P(n) |
|---|---|
| 1 | 0 |
| 10 | .117 |
| 23 | .507 |
| 50 | .970 |
| 70 | .999 |
Birthday line
At a movie theater, the manager announces that they will give a free ticket to the first person in line whose birthday is the same as someone who has already bought a ticket. You have the option of getting in line at any time. What position in line gives you the greatest chance of being the first duplicate birthday?
Assume that you don’t know anyone else’s birthday, and that birthdays are distributed randomly throughout the year.
Position 20.
Proof
Your probability of getting a free ticket when you are the nth person is line is (probability that none of the first n-1 people share a birthday) \(\times\) (probability that you share a birthday with one of the first n-1 people):
\[P(n) = \frac{365 \times 364 \times ... \times (365-(n-2))}{365^{n-1}} \frac{n-1}{365}\]We want the first \(n\) such that \(P(n) > P(n+1)\):
\[\begin{align} \frac{365 \times 364 \times ... \times (365-(n-2))}{365^{n-1}} \frac{n-1}{365} & > \frac{365 \times 364 \times ... \times (365-(n-2)) \times (365-(n-1))}{365^n} \frac{n}{365} \\ 365 (n-1) & > (365 - (n-1)) n \\ n^2 - n - 365 & > 0 \end{align}\]Solving for \(n\) we find roots at \(n \approx -18.6\) and \(n \approx 19.6\). The negative root is invalid for this problem.
Thus we need \(n > 19.6\) giving a minimum of \(n = 20\).
Caterpillar on a bungee
A caterpillar crawls along a very flexible 1 m long bungee cord. It starts off at one end of the bungee cord, and starts crawling to the other end. When the caterpillar has crawled 1 cm, the bungee cord extends by a meter to 2 m. When the caterpillar has crawled another 1 cm, the bungee cord extends by another meter to 3 m. This continues on, each time the caterpillar progresses by 1 cm, the bungee cord extends by another meter.
Will the caterpillar ever reach the other side?
Note that as the bungee cord is stretched, the caterpillars relative position on the cord remains the same, its absolute position increases.
Yes, the caterpillar does reach the other side, eventually.
Proof
Because the relative position of the caterpillar remains the same when the bungee cord is stretched, we will look at the position of the caterpillar as a fraction of the bungee cord length, \(L\). It starts at position \(0L\), and must reach position \(1L\).
In the first step, the caterpillar walks \(\frac{1}{100} L\). In the next step, the caterpillar walks \(\frac{1}{200} L\), then \(\frac{1}{300} L\), and so on. The total distance the caterpillar has travelled after \(n\) steps is:
\[\sum_{x=1}^n \frac{1}{100 x} L = \frac{L}{100} \sum_{x=1}^n \frac{1}{x}\]We require the distance to equal \(1L\) for the caterpillar to reach the other side, hence we need some \(n\) such that:
\[\begin{align} L & < \frac{L}{100} \sum_{x=1}^n \frac{1}{x} \\ 100 & < \sum_{x=1}^n \frac{1}{x} \end{align}\]\(\sum_{x=1}^n \frac{1}{x}\) is the harmonic series, which diverges. Thus it will eventually exceed 100 for some (very large) value of \(n\). Therefore the caterpillar will reach the other side. In general, this is true for any length cord.
By the Euler-Maclaurin formula, the harmonic series is approximated by:
\(H_n \approx \ln n+\gamma\) where \(\gamma \approx 0.5772\)
We need to reach \(H_n > 100\). Thus an approximation for the number of steps taken by the caterpiller is:
\[n \approx e^{H_n - \gamma} \approx 1.5 \times 10^{43}\]Chameleons
On a remote island there are population of rare chameleons, each one being either red, green or blue. If two different coloured chameleons meet then they will both change to the third colour. For example, if a red chameleons meet a blue on, they will both turn green. Initially their numbers are as follows:
- 13 red chameleons
- 15 green chameleons
- 17 blue chameleons
Is it ever possible for all the chameleons to become the same colour?
No, the chameleons can never all be the same colour.
Proof
Let \(c_B\) be the number of blue chameleons, \(c_G\) be the number of green chameleons, and \(c_R\) be the number of red chameleons.
Let’s look at the number of each colour modulo 3. For any arrangement of colours \(i\), \(j\) and \(k\) at any time \(t\) the number of chameleons, \(N_t\) is:
\[N_t \equiv \{ c_i, c_j, c_k\} \pmod 3\]Now let’s assume a chameleon of colour \(i\) and \(j\) meet, by our rules the new numbers are:
\[\begin{align} N_{t + \Delta t} & \equiv \{ c_i - 1, c_j - 1, c_k + 2\} \pmod 3 \\ & \equiv \{ c_i - 1, c_j - 1, c_k - 1\} \pmod 3 \end{align}\]Thus the difference between the numbers can never change (modulo 3).
Initially we have:
\[N_0 \equiv \{ c_R, c_G, c_B\} \equiv \{ 1, 0, 2\} \pmod 3\]For all the chameleons to be the same colour we would require the other two colours to both have 0 chameleons. However, from our initial condition this can never happen because none of the initial numbers are the same modulo 3.
Colliding ants
You have an large supply of ants. Each ant moves at 1 m/s. When two ants collide, they reverse directions.
Ants on a stick
Suppose you have a 1m long stick. On the stick are ants, randomly placed and facing left or right randomly. When an ant reaches either end end of the stick, it falls off.
Find the upper limit of the time it takes for the stick to be clear of ants, regardless of the original setup.
The stick will be clear of ants in, at most, 1 second.
Proof
When two ants reverse direction, it is equivalent to the two ants moving past each other because the identity of each ant doesn’t matter. Thus for the 1m long stick, all ants will have fallen off after 1 second.
Ants on a ring
Suppose you have a ring with a circumference of 1 m. There are 100 ants evenly spaced, 1 cm apart from each other on the ring. The ant are numbered in clockwise order so that #2 is just clockwise of #1, and #1 is just clockwise of #100, etc. At time \(t = 0\), all the prime-numbered ants (#2, #3, #5, … #97) start walking clockwise, while the other ants start walking counter-clockwise.
How far from its starting position is ant #1 at time \(t=1\) second?
Ant #1 and will have moved 50 cm counter-clockwise along ring (it will be on the opposite side of the ring).
Proof
As with the ants on a stick, two ants colliding is equivalent to them passing past each other if we don’t care about their identities. Thus at \(t=1\) there will be an ant on each of the position where there was \(t=0\), though this maybe a different ant to the original ant.
However, since the ants actually reverse direction when they collide, the relative order of the ants remain unchanged. Ant #1 remains between #2 and #100, ant #2 remains between #1 and #3, etc.
Since all ants end on one of the starting points at \(t=1\), ant #1 shifts counter-clockwise by \(x\) cm for some integer \(-100 \le x \le 100\). Because the relative order of the ants remains the same, and there is an ant on each of the original positions at \(t=1\), all ants must have shifted counter-clockwise by the same distance \(x\) cm.
At any point in time, 25 ant are moving clockwise and 75 ants are moving counter-clockwise as there are 25 prime numbers in the first 100 positive integers. This gives a total velocity of all the ants of 50 cm/s counter-clockwise for any time \(t\). Thus at time \(t=1\) the ants will all have moved counter-clockwise by 50 cm, meaning each individual ant will have moved counter-clockwise by 50 cm.
Everything equals 6
Make the following statements true by only adding mathematical operators:
\[\begin{align} 0 \quad 0 \quad 0 & = 6 \\ 1 \quad 1 \quad 1 & = 6 \\ 2 \quad 2 \quad 2 & = 6 \\ 3 \quad 3 \quad 3 & = 6 \\ 4 \quad 4 \quad 4 & = 6 \\ 5 \quad 5 \quad 5 & = 6 \\ 6 \quad 6 \quad 6 & = 6 \\ 7 \quad 7 \quad 7 & = 6 \\ 8 \quad 8 \quad 8 & = 6 \\ 9 \quad 9 \quad 9 & = 6 \end{align}\]For example \(2 + 2 + 2 = 6\).
\[\begin{align} (0! + 0! + 0!)! & = 6 \\ (1 + 1 + 1)! & = 6 \\ 2 + 2 + 2 & = 6 \\ 3 \times 3 - 3 & = 6 \\ 4 + 4 - \sqrt{4} & = 6 \\ 5 + 5 / 5 & = 6 \\ 6 + 6 - 6 & = 6 \\ 7 - 7 / 7 & = 6 \\ \left(\sqrt{8 + 8 / 8}\right)! & = 6 \\ (9 + 9) / \sqrt{9} & = 6 \end{align}\]
An interesting thing to note is that if we had four numbers instead of three then for any \(x \ne 0\):
\[\left((x + x + x) / x\right)! = 6\]Factorial zeros
How many zeros are there in 100!?
100! is 100 factorial, which is all the numbers up to 100 multiplied togther.
100! has 24 zeros.
Proof
The number of zeros at the end of a number tells us how many times 10 divides into the number. Each 10 that divides a number can be broken down into a 5 and a 2.
For factorial, factors of 2 are very common - every even number adds at least one 2. Thus for every 5, there will always be a 2 available. Therefore we only need to count how many times 5 goes into the factorial.
Every multiple of 5 introduces another 5 to the factorial’s factors. There are \(\left\lfloor \frac{n}{5} \right\rfloor\) 5s in the numbers up to \(n\). However, we also need to count an extra 5 for every multiple of \(5^2\), and so on for all powers of 5. We can only stop when the powers of 5 exceed \(n\).
Thus to calculate the number of times 5 divides \(n!\), and thus the number of zeros at the end, we have:
\[\sum_{i=1} \left\lfloor \frac{n}{5^i} \right\rfloor\]For \(n=100\):
\[\left\lfloor \frac{100}{5} \right\rfloor + \left\lfloor \frac{100}{25} \right\rfloor = 20+4 = 24\]Friends at a party
There is a party with a large number of people. Some people at the party are friends, some aren’t. All friendships are mutual.
Number of friends
Show that there are at least two people at the party who have the same number of friends.
Let \(n\) be the number of people at the party.
Since no one can be friends with themselves, everyone has between 0 and \(n-1\) friends.
If someone has \(n-1\) friends then that person is friends with everyone else, so no one can have 0 friends.
Likewise if someone has 0 friends, no one can have \(n-1\) friends (be friends with everyone).
Thus there are \(n-1\) possible numbers of friends and \(n\) people, so by the pigeon-hole principal, at least two people have the same number of friends.
Mutual friends
Now show that any group of six people contains either 3 mutual friends or 3 mutual strangers.
Imagine the 6 people. Of them, some person \(X\) either has at least 3 friends among the other 5, or at least 3 strangers.
If \(X\) has at least three friends, then either:
- The 3 of them are all mutual strangers.
- At least 2 of them are friends. Then the these 2 and \(X\) are all mutual friends.
Both of these satisfy the condition.
If \(X\) has at least three strangers, then either:
- The 3 of them are all mutual friends.
- At least 2 of them are strangers. Then the these 2 and \(X\) are all mutual strangers.
Both of these also satisfy the condition.
General case
In general, if we require there be either a group of \(a\) mutual strangers or \(b\) mutual friends then the minimum sized group of people required is called the Ramsey number: \(R(a,b)\). The case explored in this problem is \(R(3,3) = 6\).
Fuel circuit
\(N\) fuel canisters are placed along a race track. In total they contain \(L\) liters of fuel.
Suppose a race car needs \(L\) liters of fuel to go around the race track once. The cars fuel milage only depends on the distance travelled. The car can hold more than \(L\) liters of fuel.
Prove that there exists at least point on the cicuit from which the car can complete a full lap, starting with an empty tank of fuel.
Given \(N\) canisters, there is at least one canister with enough fuel to reach the next canister. Otherwise the total fuel in the canisters would not be sufficient to make it around the circuit.
Combine the next canister with the current canister at the location of the current canister, such that there are now \(N-1\) canisters. The total fuel is still \(L\). If the problem can be solved with these \(N-1\) canisters, the original problem can be solved since we’ve established that there was enough fuel to reach the next canister.
Now the same reasoning can be used to reduce the problem down to 1 canister which contains all \(L\) liters of fuel, at which point the problem is trivial.
Choosing this as the starting point allows us to solve the original problem.
Hidden ages
Alice is telling Bob about her children. Alice says she has three daughters and that the sum of their ages is the number of the house across the street.
Bob asks what their ages are.
Instead of answering directly, Alice tells Bob that the product of their ages is 36.
Bob says that this is not enough information to determine their ages.
Alice agrees and adds that the oldest daughter has the beautiful blue eyes.
Bob now knows the ages of Alice’s daughters.
How old are Alice’s daughters?
The daughters are 2, 2 and 9 years old.
Proof
The possible ages that multiply to 36 are (along with their sums):
- 1, 1, 36 (38)
- 1, 2, 18 (21)
- 1, 3, 12 (16)
- 1, 4, 9 (14)
- 1, 6, 6 (13)
- 2, 2, 9 (13)
- 2, 3, 6 (11)
Bob knows the sum of the ages because he can see the house number. Since knowing the sum is not enough to determine the ages, the sum must be one of the sums that is not unique.
The only sum that is not unique is 13, which is the sum of (1, 6, 6) and also (2, 2, 9).
Next Alice tells Bob about her oldest daughter. This means that the ages cannot be (1, 6, 6), since there is no oldest daughter in this case.
Hence the ages are 2, 2 and 9.
Hidden polynomial
I choose a polynomial with non-negative integer coefficients. You don’t know how many coefficients are in the polynomial. Your goals is to find out what my polynomial is. You are only allowed to ask me to evaluate the polynomial at integer points.
What is the fewest number of queries you can ask to determine my polynomial?
Only 2 queries are required.
Proof
Let the polynomial you are trying to guess be \(p(x) = \sum c_i x^i\).
First, attempt to determine \(p(x)\) with only one query: \(a\). This would not allow us to distinguish between the polynomials \(p_1(x) = x\) and \(p_2(x) = a\) - both would evaluate to \(a\).
To solve the problem with two queries, first ask for \(p(1)\):
\[r_1 = p(1) = \sum c_i\]Let \(b=r_1+1\). Since the coefficients of \(p(x)\) are non-negative, \(b\) is greater than all \(c_i\).
Next evaluate \(p(b)\):
\(r_2 = p(b) = \sum c_i b^i\).
The coefficients of the polynomial can be read off as the digits of \(r_2\) when it is written in base \(b\).
Hidden vector
In a very similar problem I have a hidden vector of \(n\) non-negative integers \([x_1, x_2, \ldots, x_n]\). Your goal is to find out my vector. You are allowed to name any vector \([y_1, y_2, \ldots, y_n]\) of \(n\) non-negative integers, and I’ll tell you the dot product of your vector and my vector.
Clearly by naming the \(n\) vectors \([1, 0, \ldots, 0], [0, 1, \ldots, 0], \ldots, [0, 0, \ldots, 1]\) you can find my vector.
What is the fewest number of vectors required for you to be sure of my vector?
Only 2 vectors are required.
Proof
Let the vector you are trying to guess be \(\mathbf{x} = [x_1, x_2, \ldots, x_n]\).
First, attempt to determine \(\mathbf{x}\) with only one query, \(\mathbf{y} = [y_1, y_2, \ldots, y_n]\). Assume \(n > 1\). All entries in \(\mathbf{y}\) must be non-zero. If some value \(y_i\) was zero, then we would have no information about entry \(x_i\). However, now we cannot tell the difference between the vectors \(\mathbf{x} = [y_2, 0, x_3, x_4, \ldots, x_n]\) and \(\mathbf{x} = [0, y_1, x_3, x_4, \ldots, x_n]\). Both result in the dot product of \(\mathbf{x} \cdot \mathbf{y} = y_1 y_2 + \sum_{i=3}^n y_i x_i\).
Thus we must use at least 2 vectors, \(\mathbf{y}_1\) and \(\mathbf{y}_2\). Let \(\mathbf{y}_1 = [1, 1, \ldots, 1]\). This will result in the value \(r_1\) which is the sum of all values in \(\mathbf{x}\):
\[r_1 = \mathbf{x} \cdot \mathbf{y_1} = \sum_{i=1}^n x_i\]Let \(b = r_1+1\). Since the values in \(\mathbf{x}\) are non-negative, \(b\) is greater than all \(x_i\).
Now construct our second vector \(\mathbf{y}_1 = [1, b, b^2, b^3, \ldots, b^{n-1}]\). Our second result, \(r_2\) will be:
\[r_2 = \mathbf{x} \cdot \mathbf{y_2} = \sum_{i=0}^{n-1} x_{i+1} b^i\]The numbers \(x_i\) can be read as the digits of \(r_2\) when it is written in base \(b\).
Open lockers
A school has a hallway with 100 lockers. All the lockers are closed.
A student walks down the hallway can opens every locker. A second student walks down the hallways and closes every second locker, starting at locker 2. A third student then walks down the hallways and changes the state of every third locker, starting at locker 3.
The \(n\)th student walking down the hallway changes the state of every \(n\)th locker starting at locker \(n\).
After 100 students have passed down the hallway, which lockers are open?
The lockers left open are the square numbers: 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100.
Proof
The lockers that are left open are those that have been changed an odd number of times.
Since student \(n\) changes all the lockers that have \(n\) as a factor, the lockers that have changed are those that have an odd number of factors.
Factors come in pairs (\(n = f_1 \times f_2\)), so for there to be an odd number of factors, a factor \(f\) must repeat itself in a pair (\(f = f_1 = f_2\)). In this case \(n = f \times f\), thus \(n\) is a square number.
Monkey and the coconuts
Five sailors were shipwrecked on an island with coconuts trees and a monkey. They spent the first day gathering coconuts. During the night, one sailor woke up and decided to take his share of the coconuts. He divided them into five piles. One coconut was left over so he gave it to the monkey, then hid his share, put the rest back together, and went back to sleep.
Soon a second sailor woke up and did the same thing. After dividing the coconuts into five piles, one coconut was left over which he gave to the monkey. He then hid his share, put the rest back together, and went back to bed. The third, fourth, and fifth sailor followed exactly the same procedure. The next morning, after they all woke up, they divided the remaining coconuts into five equal shares. This time no coconuts were left over.
How many coconuts were there in the original pile?
3121 coconuts in the minimum size of the original pile.
Proof
Each time a sailor visits the pile, one coconut is lost (to the monkey) and the size of the pile is reduced by \(\frac{1}{5}\)th. Thus the size of the pile goes from \(N \rightarrow \frac{4}{5}(N - 1)\).
Iterating this formula gets unwieldy, so we first rewrite it as the following equivalent formula: \(N \rightarrow \frac{4}{5}(N + 4) - 4\).
Now iterating the formula 5 times (once for each sailor) gives the following sequence:
\[\begin{align} N & \rightarrow \frac{4}{5}(N + 4) - 4 \\ & \rightarrow \frac{16}{25}(N + 4) - 4 \\ & \rightarrow \frac{64}{125}(N + 4) - 4 \\ & \rightarrow \frac{256}{625}(N + 4) - 4 \\ & \rightarrow \frac{1024}{3125}(N + 4) - 4 \end{align}\]Since that number of coconuts in the final pile must be an integer and 1024 is relatively prime to 3125, \(N+4\) must be a multiple of 3125. The smallest such multiple is 3125 \(\times\) 1, so \(N\) = 3125 – 4 = 3121. The number left in the morning comes to 1020, which is evenly divisible by 5 as required.
See Monkey and the coconuts on Wikipedia for other proofs and variations of the problem.
Hiking in the mountains
At 6 am you start hiking on a path up a mountain. You walk at a variable pace, resting occasionally. At 6 pm that day you reach the top of the mountain. You camp out overnight.
The next morning you wake up at 6 am and start your descent down the mountain. Again you walk down the path at a variable pace, resting occasionally. The downhill hike is easier, but you are tired after yesterday and at 6 pm you reach the bottom.
Is it possible to find some time during the second day, such that you are at the exact same spot you were on at the same time on the first day?
You can always find a spot such that you were there at the same time on both the first and the second day.
Proof
Imagine a second hiker, who starts climbing the same path at 6 am on the second day. Now assume that the second hiker walks at exactly the same speed you did on the first, and takes the same breaks you did.
Now on the second day, since you both start at opposite ends of the path at 6 am and finish at opposite ends at 6 pm, you must have met each other along the way. The point where you meet gives a point where you were at the same position at a given time on both days.
Negating function
Design a function \(f: \mathbb{Z} \rightarrow \mathbb{Z}\) such that \(f(f(n)) = -n\).
An example is:
\[f(n) = \operatorname{sgn}(n) - n(-1)^n\]Proof
Suppose that \(f(x) = y\) for some \(x\) and \(y\). Then:
\[\begin{align} f(y) = & f(f(x)) = -x \\ f(-x) = & f(f(y)) = -y \\ f(-y) = & f(f(-x)) = x \\ \end{align}\]Therefore continued application of \(f\) results in a cycle: \(x \rightarrow y \rightarrow -x \rightarrow -y \rightarrow x\).
This implies that \(f(0) = 0\) because we require that \(x = f(0) = f(-0) = -x\).
For all other integers we need to partition them into groups of 4, each which contain some \(x\), \(y\) and their negations. To construct such a mapping, let us make the simplest choice of letting \(f(1) = 2\). This then forces the following cycle: \(1 \rightarrow 2 \rightarrow -1 \rightarrow -2 \rightarrow 1\).
Likewise we can let \(f(3) = 4\) and in general for \(k > 0\) we can let \(f(2k-1) = f(2k)\) which forces: \(2k-1 \rightarrow 2k \rightarrow -2k-1 \rightarrow -2k \rightarrow 2k-1\). Thus we can define how the function acts on a number based on whether it is positive or negative and whether it is even or odd:
\[f(n) = \begin{cases} n + 1 & \text{ if } n > 0 \wedge n \text{ is odd} \\ -n + 1 & \text{ if } n > 0 \wedge n \text{ is even} \\ n - 1 & \text{ if } n < 0 \wedge n \text{ is odd} \\ -n - 1 & \text{ if } n < 0 \wedge n \text{ is even} \end{cases}\]When \(n < 0\) we are always adding 1, and when \(n > 0\) we are always subtracting \(1\). Thus the above simplifies to:
\[f(n) = \begin{cases} \operatorname{sgn}(n) + n & \text{ if } n \text{ is odd} \\ \operatorname{sgn}(n) - n & \text{ if } n \text{ is even} \end{cases}\]Now \((-1)^n = 1\) when \(n\) is even, and \((-1)^n = -1\) when \(n\) is odd. This allows us to simplify the above to our solution: \(f(n) = \operatorname{sgn}(n) - n(-1)^n\)
By construction it satisfies \(f(f(n)) = -n\) for \(n \ne 0\), and we can evaluate \(f(0)\) to check that it indeed holds for \(0\) as well. Thus our solution is correct.
Burning fuses
You have a lighter and two fuses. Each fuse takes an hour to burn, but they don’t burn at a steady rate throughout the hour.
How do you use the two fuses to create a 45 minute timer?
Light both ends of the first fuse and one end of the second fuse. When the first fuse has completely burnt, light the other end of the second fuse. When the second fuse has completely burnt, 45 minutes has passed.
Proof
When both ends of a fuse are lit, the fuse will burn in half the time. This is true however unevenly the fuse burns.
The first fuse will burn out completely in 30 minutes. At that time the second fuse is now has 30 minutes remaining.
We can think of the second fuse now as 30 minute fuse. If we light the other side, it will burn out in half the time: 15 min. Thus 30 + 15 = 45 minutes will have passed.
Extensions
In this problem we measured out a time which was \(\frac{3}{4}\) of the total fuse length.
In general the times we can measure with some number of fuses which burn in a unit length of time are called Fusible numbers.
Hourglasses
You have 2 hourglasses, a 7-minute timer and a 11-minute timer.
How do you use these to time 15 minutes?
Follow these steps:
| Time (minutes) | Action |
|---|---|
| 0 | Start both timers. |
| 7 | When the 7-minute timer finishes turn it upside-down. |
| 11 | When the 11-minute timer finishes turn, turn the 7-minute timer upside-down. At this point it has 4 minutes of sand at the top. |
| 15 | When the 7-minute timer finishes, you are done. |
Note, that this assumes that a half-finished timer will measure the same time when turned upside-down. This may not be true in physical systems. (For real hourglasses with sand, this is going to be accurate enough).
To solve the puzzle without this assumption, set-up 7 minutes before you need to start timing:
| Time (minutes) | Action |
|---|---|
| -7 | Start both timers. |
| 0 | When the 7-minute timer finishes, your time starts. |
| 4 | When the 11-minute timer finishes, turn it upside-down. |
| 15 | When the 11-minute timer finishes again, you are done. |
Marble bags
You have 100 bags of 100 marbles. All of the marbles in all of the bags are identical 1 gram marbles, except for one of the bags, which contains marbles that weigh 1.001 grams. You have a scale that can to an accuracy of 0.001 grams.
What is the minimum number of weighings required to identify the bag with the slightly heavier marbles?
You only need 1 weighing.
Proof
Number each bag from 1 to 100. Onto the scale put \(i\) marbles from bag #\(i\). That is put 1 marble from bag #1, 2 marbles from bag #2 and so on.
The total number of marbles, \(M\), on the scale is:
\[\begin{align} M & = \sum_{i=1}^{100} i \\ & = \frac{100 (100 + 1)}{2} \\ & = 5050 \end{align}\]The difference between the actual weight and 5050 grams divided by 0.001 will give you the number of the bag with the slightly heavier marbles.
Marble scales
8 marbles
You have 8 marbles and a balance scale. All the marbles have the same weight, except one which is slightly heavier.
How do you determine which is the heavy marble in the minimum number of weighings.
We can do it in 2 weighings.
If we only have 3 marbles, we can determine the heaviest with one just weighing: Put a marble on each side of the scale, and leave one aside.
- If the scale is unbalanced then the heavier side is the heavy marble.
- Otherwise the marble left aside is the heavy marble.
To solve the problem for 8 marbles, first weigh 3 marbles on each side of the scale, leaving 2 aside:
- If the scale is unbalanced, take the 3 marbles on the heavy side and determine the heavy marble with one weighing as above.
- Otherwise weigh the 2 remaining marbles to determine which is heavier.
12 marbles
You have 12 marbles and a balance scale. All the marbles have the same weight, except one which is different. The odd marble may be either heavier or lighter.
How do you determine which is the odd marble in the minimum number of weighings. You must also determine whether it is heavier or lighter.
Note: This is difficult and the solution is not intuitive. It is included because it is a very wide-spread puzzle.
We can do it in 3 weighings.
First note, that if we have 3 marbles with 1 odd marble then we can find the odd marble in one weighing if we know that the odd marble is heavier or lighter. Simply weigh 2 of the 3. If the scale is unequal then we’ve identified the odd marble, otherwise the odd marble is the remaining marble.
First group the marbles into 3 groups of 4. Weigh 2 of the groups:
- If the groups are of equal weight:
- Mark all eight marbles weighed as good.
- Take 3 of the 4 remaining marbles and weigh them against 3 good marbles:
- If the two sides wiegh the same then the last marble is the odd marble. Weigh it against a good marble to determine if it heavier or lighter.
- If the two sides are unequal, then we know that the odd marble is in the group of 3, and we know whether it is heavier or lighter. This is just the 3 marble case which can be solved in one weighing.
- If the groups are unequal:
- The 4 remaining marbles are good.
- From the scale we have a heavy group of 4 and a light group of 4.
- Now will weigh 3 marbles from the light group and one from the heavy group
against 3 good and 1 from the light group:
- If the side with 3 light and 1 heavy is heavier then the odd marble is either the 1 from the heavy group, or the 1 from the light group on the light side. Comparing either of these with a good marble will identify the odd marble.
- If the side with 3 light and 1 heavy is lighter, then one of the 3 from the light group is the odd marble. This is just the 3 marble case which can be solved in one weighing.
- If the scale is equal then the odd marble is one of the 3 remaining marbles from the heavy group. This is just the 3 marble case which can be solved in one weighing.
General case
In the general case there are \(N\) marbles with one odd marble. We may or may not know whether the odd ball is heavier or lighter.
The general case solution is explored in this math stackexchange post.
⇪Melted water bottle
Two people are alone in a desert, and they have one full bottle of water between them. The water bottle is clear and plastic. The water bottle has been deformed by the heat and hence it is hard to gauge how much liquid it actually holds. They agree to each drink half of it each.
The first person takes a drink, then hands the bottle to the second person. However, the second person thinks the first person drank more than their fair share.
How can they check? They haven’t got any other containers, so they can’t pour any of the water out.
Person two notes where the water level is on the bottle. They can do this by making a mark, or simply keeping their finger there. They then turns the bottle upside down (with a lid on). If there the water level is below the place that was noted earlier, then person one drank more than their fair share.
Water jugs
You have 8 liters of water in a jug and you want to split it evenly into two lots of 4 liters.
You have 2 other water jugs which hold 3 and 5 liters each. None of the jugs have any markings.
How can you measure out 4 liters?
Follow these instructions:
- Fill the 5-liter jug from the 8-liter jug.
- Fill the 3-liter jug from the 5-liter jug.
- Pour the 3-liter jug in the 8-liter jug.
- Pour the 2 remaining liters from the 5-liter jug to the 3-liter jug.
- Fill the 5-liter jug from the 8 liter-jug.
- Fill the 3-liter jug from the 5-liter jug. Since only 1 more liter fits in the 3-liter jug, there will be 4 liters left in the 5-liter jug.
- Pour the 3-liter jug into the 8-liter jug.
Since we haven’t lost any water, there is now 4 liters in the 5-liter jug, and hence the other 4-liters in the 8-liter jug.
General case
You have two water jugs which each hold \(A\) and \(B\) liters of water respectively. Both \(A\) and \(B\) are integers and the water jugs have no markings. You can fill the jugs as much as you want from a tap.
What are the quantities can you measure out if both jugs start out empty?
You can measure out any multiple of \(\gcd(A, B)\).
Proof
First note that at the end of any action, both jugs can’t be partially full. There are no markings on the jugs, so we can only stop pouring when either the source is empty or the destination is full. Thus is it is never useful to empty a partially full jug - that would just leave us with the other jug completely full or empty which can be reached directly from the start.
This leaves the only useful actions as:
- Fill an empty jug
- Empty a full jug
- Pour a full jug into the other jug until either the other jug is full, or the first jug is empty
Let \(a\) and \(b\) be the current amounts of water in jug \(A\) and \(B\) respectively. If we plot the valid paths on a cartesian grid, then valid region that we can be within is along the perimeter where \(a=0\), \(a=A\), \(b=0\) or \(b=B\). This forms a rectangle.
Valid paths in this space will be:
- Horizontal lines between the top and bottom edges: Filling or emptying jug \(A\)
- Vertical lines between the left and right edges: Filling or emptying jug \(B\)
- Negative diagonal lines from one side to the another: Pouring one jug into the other.
Instead of the moving horizontally or vertically, we can instead imagine it continuing in a straight line into a copy of the rectangle. In this case, the real quantities will be given by \(a \mod A\) and \(b \mod B\) to bring as back into the original rectangle:
Since we start with empty jugs, all valid paths start at \((0, 0)\), hence all valid paths can be mapped to the negative diagonal line \(a = -b\).
The strategy
Traveling up along the negative diagonal corresponds to the following strategy:
- If \(A\) is empty, fill \(A\)
- If \(B\) is full, empty \(B\)
- Otherwise pour as much water as possible from \(A\) into \(B\).
- Stop when you have the required quantity.
Traveling down along the line simply swaps \(A\) and \(B\) in this strategy. This will reach all possible values.
Valid values
Suppose the final quantity is in jug \(B\). Then jug \(A\) is either full or empty and in either case \(a = 0 \mod A = x A\) for some integer \(x\). \(b\) can also be written as \(b' + y B\) for some integer \(y\). In combination with our path equation:
\[\begin{align} a = -b & = 0 \mod A \\ b & = x A \\ b' + (-y) B & = x A \\ b' & = x A + y B \end{align}\]By Bézout’s theorem the values of \(b'\) that satisfy this are the multiples of \(\gcd(A, B)\). By symmetry we get the same result if we want the final quantity to finish in jug \(A\).
If the desired quantity doesn’t fit in a single jug then we can first measure out and keep aside a multiple of either \(A\) or \(B\) and then follow the strategy above once the required value fits in a single jug.
More than 2 jugs
This extends to more than 2 jugs. See a discussion here.
Airport walkway
Stopping
You are at an airport and are approaching a moving walkway. You look down and realize you need to tie your shoe.
Assuming you want to lose as little time as possible, should you stop now to tie your shoelace or wait until you are on the walkway.
Wait until you are on the walkway.
Proof
Imagine two people walking together at the same speed. One stops right before the walkway, and the other stops right as the walkway starts. That is, they stop very close to each other.
However, while they are stopped the person on the walkway continues moving and increases the distance between the two. When they both start walking again (at the same time) now they are separated by the distance that the walkway has moved during this time.
Since they walk at the same speed, this separation will remain.
Sprinting
Now you are on the walkway, but are late since you stopped to tie your shoe. You decide to sprint, but you can only sprint for a short burst, and only once.
Should sprint on the moving walkway or wait until you are off?
Wait until you are off the walkway to sprint.
Proof
- Let your walking speed be \(v\)
- Let your sprinting speed be \(v'\).
- Let the length of time you sprint be \(t\).
- Let \(w\) be the the walkway speed.
Assume if you sprint on the walkway then the entire sprint talks place on the walkway. If any sprinting occurs after the walkway, that doesn’t correspond to any change in separation.
We compare the time saved in each scenario compared not sprinting:
- If sprinting off the walkway you sprint for a distance \(d = v't\). This would have taken a time \(t+\Delta t = \frac{d}{v}\) to walk. The time saved is: \(\Delta t_1= \frac{v't}{v}-t = t\left(\frac{v'}{v}-1\right)\).
- If sprinting on the walkway you sprint for a distance \(d = (v'+w)t\). This would have taken a time \(t+\Delta t = \frac{d}{v+w}\) to walk. The time saved is: \(\Delta t_2= \frac{(v'+w)t}{v+w}-t = t\left(\frac{v'+w}{v+w}-1\right)\).
We want to sprint off the walkway if \(\Delta t_1 > \Delta t_2\):
\[\begin{align} t\left(\frac{v'}{v}-1\right) & > t\left(\frac{v'+w}{v+w}-1\right) \\ \frac{v'}{v} & > \frac{v'+w}{v+w} \\ v'(v+w) & > v(v'+w) \\ v'v+v'w & > vv'+wv \\ v' & > v \end{align}\]Since you sprint faster than you walk, you should sprint once off the walkway.
Note that the converse also holds. If you want to slow down (or stop completely as in the first part), then do so on the moving walkway.
Apple delivery
You have 3000 apples. You wish to transport them to a town 1000 km away. A friend offers to help you with this. His car can hold 1000 apples at most. However, he loves apples, so if there are any apples in the car, then he will eat 1 every kilometre that he travels.
You can store apples at any arbitrary point along the way. If your friend has a partially eaten apple at the end of a trip he will finish the rest of it off.
What is the maximum number of apples you can transport to the other town?
We can get 833 apples to the other town.
Proof
Let the town you are in be town #1 and the destination be town #2. Let the distance between them be \(D\), and the number of apples be \(A\), and the capacity of the car be \(C\) apples.
A couple of observations:
- Since our friend will finish of a partially eaten apple, there is no benefit in travelling non-integer distances.
- If our friend travels a distance \(d_1\), then they could equally travel the same distance in two steps. First travel a distance \(d_0 < d_1\), then travel the rest of the distance. The apples can even be stored at \(d_0\) while the friend does other things.
Taking these together, we can consider the problem 1 km at a time. Thus we just need to determine the most efficient way to transport \(a\) apples 1 km.
Given that a 1 km trip can’t be broken up and that each trip will cost exactly 1 apple, we need to minimize the number of trips. To do this we fill up the car as much as possible (up to \(C\) apples) for each trip, giving us:
\[n = \left\lceil \frac{a}{C} \right\rceil\]Where \(n\) is the number of car trips, and the number of apples eaten. Afterwards, there will be \(a-n\) apples left. Now we can calculate the number of apples at any distance with:
\[a_0 = A\] \[a_{d+1} = a_d - \left\lceil \frac{a_d}{C} \right\rceil\]In our case, \(a_0 = 3000\) gives \(a_{1000} = 833\).
We can simplify the calculation by realizing that while \(\left\lceil \frac{a_{d+1}}{C} \right\rceil = \left\lceil \frac{a_d}{C} \right\rceil\) we don’t need to set the apples down as the number of trips will remain the same.
Thus we can travel as far as we can until the apples can be split across one fewer trips - when the total number of apples is the next lower multiple of \(C\). The distance traveled is determined by the number of apples we have to spare and the number of trips:
\[d = \begin{cases} \frac{C}{\left\lceil \frac{a}{C} \right\rceil} \text{ if } a \mid C \\ \frac{a \mod C}{\left\lceil \frac{a}{C} \right\rceil} \text{ if } a \nmid C \end{cases}\]Because we only deal with integer distances, if we are required to go a non-integer distance \(d\) we round up.
Applying this strategy to our problem:
- Stage 1
- Take 1000 apples at a time to \(d = \left\lceil \frac{1000}{3} \right\rceil = 334\)
- We now have 1998 apples left, at a distance of 334 km
- Stage 2
- Take 998 apples a further \(d = \frac{998}{2}= 499\)
- We now have 1000 apples left at 833 km
- Stage 3
- Take 1000 apples until the end, which is \(d = 167\) km away
- We end up with 833 apples at the destination.
Greedy pirates
A group of pirates have found a treasure chest containing gold coins. They are trying to divide up the treasure in the following way:
- The eldest pirate suggests a split
- All pirates vote on the split, including the eldest
- If at least half the pirates agree with the split, then it stands
- If a majority of the pirate disagree the eldest pirate is fed to the sharks, and the process continues with the second eldest pirate
Assume the pirates are perfectly logical and are trying to get as much gold as possible. They value their own lives more than any amount of gold. However, all else being equal, they would rather see more pirates dead.
100 pirates, 1000 coins
If there are 100 pirates in the group, and the treasure chest contains 1000 coins, how much gold does the eldest pirate end up with?
The eldest pirate ends up with 951 gold coins.
Proof
Number the pirates in order of age, so the eldest is #1000 and the youngest is #1.
Let \(P_N\) be the strategy for dividing up the \(C\) coins among \(N\) pirates. Let \(P_N(n)\) be the amount that pirate \(n\) gets when there are \(N\) pirates and pirate \(N\) proposes the optimal plan:
\[P_N = \{ n_1, n_2, \ldots, n_N \}\]We will prove via induction that the optimal strategy, \(P_N\), is:
\[\begin{align} P_N(n) & = \begin{cases} 1 & \text{ if } n \equiv N \pmod 2 \wedge n < N \\ 0 & \text{ if } n \not\equiv N \pmod 2 \wedge n < N \\ R & \text{ if } n = N \end{cases} \\ P_N & = \left\{ \ldots, 1, 0, 1, 0, R \right\} \notag \\ & \text{ where } R = C - \left\lfloor \frac{N-1}{2} \right\rfloor \notag \end{align}\]Note that we require that \(R \ge 0\). Thus this strategy is only valid for \(N \le 2 (C + 1)\).
We see that for \(P_N\):
- There is one pirate with \(R\) coins
- There are \(\left\lfloor \frac{N-1}{2} \right\rfloor\) pirates with 1 coin
- There are \(\left\lfloor \frac{N}{2} \right\rfloor\) pirates with 0 coins
Consider the case where there is only one pirate left, #1. Then he gets all \(C\) gold:
\[P_1 = \{ C \}\]We see that \(P_1\) is consistent with \(P_N\). In addition, we can write \(P_{N+1}\) as:
\[P_{N+1}(n) = \begin{cases} 0 & \text{ if } n \equiv N \pmod 2 \wedge n < N+1 \\ 1 & \text{ if } n \not\equiv N \pmod 2 \wedge n < N+1 \\ R & \text{ if } n = N+1 \end{cases}\]Now we know that if \(P_N\) is the optimal strategy, then \(P_{N+1}\) is strictly better than \(P_N\) for at least half the pirates:
\[P_{N+1} \rightarrow P_{N+1}(n) > P_N(n) \text{ for at least } \left\lceil \frac{N+1}{2} \right\rceil \text{ pirates}\]And we cannot reduce the number of coins \(R\) that pirate #\((N+1)\) gets without falsifying this equation.
Comparing \(P_N\) with \(P_{N+1}\) we see that:
- The \(\left\lfloor \frac{N}{2} \right\rfloor\) pirates who got 0 coins in \(P_N\) get 1 coin in \(P_{N+1}\)
- Pirate #\((N+1)\) who is dead in \(P_N\) gets \(R\) coins in \(P_{N+1}\)
- The other pirates all get 0 coins
Thus \(\left\lfloor \frac{N}{2} \right\rfloor + 1\) are better off under \(P_{N+1}\) than \(P_N\). We require \(\left\lceil \frac{N+1}{2} \right\rceil\) votes for \(P_{N+1}\) to be valid:
\[\begin{align} \left\lfloor \frac{N}{2} \right\rfloor + 1 = \frac{N}{2}+ 1 = \left\lceil \frac{N}{2} + \frac{1}{2} \right\rceil = \left\lceil \frac{N+1}{2} \right\rceil & \text{ for even } N \\ \left\lfloor \frac{N}{2} \right\rfloor + 1 = \frac{N-1}{2} + 1 = \frac{N+1}{2} = \left\lceil \frac{N+1}{2} \right\rceil & \text{ for odd } N \end{align}\]Thus we have exactly the amount of votes required. In addition, we used the minimum number of coins possible to secure those votes, just 1 coin to each pirate from whom we can secure a vote. Hence \(P_{N+1}\) is optimal given \(P_N\). We already have that \(P_1\) is optimal, therefore by induction the strategy \(P_N\) is optimal for all \(N \ge 1\).
In the case where \(N = 100\) and \(C= 1000\), all even number pirates other than the eldest (pirate #100) gets 1 coin each. Thus 49 coins go to these pirates. The odd numbered pirates get nothing. Finally, the eldest gets the rest which is:
\(1000 - 49 = 951\) coins.
10 pirates, 1 coin
Now, let’s have a smaller crew with only 10 pirates. However there is now only 1 gold coin. How does the eldest pirate save himself?
The eldest pirate gives the coin to 6th youngest pirate.
Proof
Again, number the pirates in order of age, so the eldest is #10 and the youngest is #1. We will look a each case from 2 to 10 pirates.
2 pirates: Pirate #2 just keeps the gold coin.
3 pirates: Pirate #3 will have to give away the gold coin, otherwise #2 and #1 will both vote against him. There is no point giving it to #2 who will get the coin anyway if pirate #3 dies. Hence he gives it to pirate #1, securing the vote from pirate #1 and thus the majority.
4 pirates: Pirate #4 can’t give a coin to pirate #1 since he will get a coin anyway if pirate #4 dies. But he can give a coin to either pirate #2 or pirate #3 and secure the majority of votes.
5 pirates: Pirate #5 can only get a maximum of 2 votes, his own, and the pirate he gives the coin to. That leaves 3 pirates who get 0 coins and thus have no incentive to vote for him. Thus pirate #5 dies, no matter what he does.
6 pirates: Pirates #6 can be guaranteed the vote of pirate #5, because pirate #5 will die otherwise. He needs one more vote. He can give a coin to either pirate #4 or pirate #1 who both receive nothing under the 4 pirate case.
7, 8 or 9 pirates: The eldest pirates in these cases have no way of getting enough votes.
10 pirates: Pirate #10 can get a votes each from #7, #8 and #9 who will all die otherwise. He can give a coin to #6 who would get nothing in the 6 pirate case. Along with his vote, he can get 5 votes, which is enough to survive.
General case
Let the number of pirates be \(N\), and the number of coins be \(C\).
\(N \le 2 (C + 1)\)
The strategy in the 100 pirate, 1000 coin case above works for any \(N \le 2 (C + 1)\).
\(N > 2C\)
We know that for \(N \le 2 C\), the eldest pirate gets at least 1 gold coin. Let us call the smallest case where the eldest pirate has to give up all coins just to survive \(N_0 = 2 C + 1\).
We have for \(N_0\) that there are \(C\) pirate who get coins, and \(C+1\) pirates who do not get coins. We also know that the \(C\) pirates who get coin in \(N_0\) don’t get any in the case \(N_0 - 1\). In addition, the \(C+1\) pirates who don’t get any coins in \(N_0\) are either dead or get one coin in \(N_0 - 1\). Thus we cannot change the arrangement of who gets given coins.
Also note that for any plan \(P_N\), if the eldest pirate dies then plan \(P_N\) is equivalent to plan \(P_{N-1}\).
Let us set up the stricter condition that a pirate \(n\) will vote against a plan \(P_N\) if there is a chance that he gets at least that much gold under \(P_{N-1}\). Call this assumption \(A\).
Let us prove via induction that:
Hypothesis: When there are \(N\) pirates, the eldest pirate has a strategy (\(P_N\)) for survival if there are at least \(C\) pirates who have no chance of receiving any gold. In addition there are at least \(C\) candidates that may receive the gold piece each.
Let us assume assume that the Hypothesis is true for some \(N\), where the eldest pirate has a strategy such that he can survive. Now consider the case \(N' > N\) to be the next case where the eldest pirate has a strategy for survival. The eldest pirate will not gain any votes by offering a gold coin to the \(C\) pirates who received one in the \(P_N\), thus those \(C\) pirates will have no chance of getting any gold under \(P_{N'}\).
The eldest pirate can gain \(C\) votes by offering a gold coin each to the \(C\) pirates who had no chance of receiving anything in \(P_N\).
Thus we have that the Hypothesis is true for \(N\), it is also true for \(N' > N\) being the next case where the eldest pirate has a strategy for survival. We can also saw that the Hypothesis is true for \(N_0\), thus the Hypothesis is true for all \(N \ge N_0\) where the eldest pirate has a strategy for survival.
Note that if we neglect assumption \(A\), then as soon as there are more than \(C\) possible pirates for the eldest pirate to give a coin to in \(P_N\) there is ambiguity in who will recieve the coins. If none of the pirates know for sure if they are getting a coin or not they would be better of with a coin in \(P_{N + 1}\). In this case, as soon as there is any doubt as to who will get the coins, the eldest pirate can give one coin to any other \(C\) pirates and secure \(C\) votes.
And thus we have that in either of these cases the eldest pirate can find \(C\) pirates who will be better of with one gold coin. In addition he will always vote for his own plan, giving:
Theorem 1: In a case \(N \le N_0\) where the eldest pirate has a strategy for survival, the eldest pirate can secure \(C+1\) votes.
The eldest pirate needs \(\left\lceil \frac{N}{2} \right\rceil\) votes to win. The only way he can secure votes of other pirates who get 0 coins are if they are guaranteed to die. Thus the preceding plan for those pirates must have failed, giving:
Theorem 2: For \(N \ge N_0\), then the eldest pirates survives if and only if the next eldest \(\left\lceil \frac{N}{2} \right\rceil - C - 1\) pirates will all fail to come up with a successful strategy.
Now let the function \(S(n) = N\) be the \(n\)th pirate who survives for all \(N \ge N_0\), where \(S(0) = N_0\). Hence we want the smallest \(S(n)\) satisfying:
\[\begin{align} S(n) - (S(n-1) + 1) & \ge \left\lceil \frac{S(n)}{2} \right\rceil - C - 1 \\ 2 S(n) - 2 \left\lceil \frac{S(n)}{2} \right\rceil & \ge 2 S(n-1) - 2 C \end{align}\]Thus we have:
\[S(n) \ge \begin{cases} 2 S(n-1) - 2 C & \text{ with } S(n) \text{ even} \\ 2 S(n-1) - 2C + 1 & \text{ with } S(n) \text{ odd} \end{cases}\]From this we can see that \(S(n)|_{even} > S(n)|_{odd}\) for any \(S(n-1)\) where \(n \ge 1\). We want the smallest \(S(n)\), hence \(S(n)\) is always even for \(n \ge 1\):
\[S(n) = 2 S(n-1) - 2 C\]Solving for \(S(n)\) with \(S(0) = N_0 = 2C + 1\) gives us:
\[\begin{align} S(n) & = 2^n S(0) - C (2^{n+1} - 2) \\ S(n) &= 2^n + 2C \end{align}\]Giving us the set of all \(N\) such that the eldest pirate survives in the case of \(N \ge N_0\) pirate:
\[N= \{2^n + 2C \mid n \in \mathbb{Z}^+ \}\]All \(N, C\)
Combining all of the above, we have that the set of all cases where there is a surviving eldest pirate is given by:
\[N_s = \{ 1 \le N \le 2C \} \cup \{N = 2^n + 2C \mid n \in \mathbb{Z}^+ \}\]For any \(N \in N_s\) the eldest pirate can live by offering \(P_N(n)\) coins to each pirate \(n\), where:
\[P_{N}(n) = \begin{cases} 1 & \text{ if } (n = N \mod 2) \wedge n < \min(N, 2 C + 1) \\ 0 & \text{ if } (n \ne N \mod 2) \vee 2 C < n < N \\ \max\left(C - \left\lfloor \frac{N-1}{2} \right\rfloor,0\right) & \text{ if } n = N \end{cases}\]This strategy is not unique for \(N > 2C + 1\).
Locked pirate chest
There is a group of 13 pirates and they want to protect their treasure chest. They decide that they should only be able to open the chest if a majority agree that it should be opened.
They ask a locksmith to come and put a specific number of locks on the chest. Each lock must be opened to open the chest. The locksmith can give as many keys as required to each pirate.
How many locks should the locksmith use, and how should the keys be distributed, such that only when the majority of pirates agree can the chest be opened?
The locksmith should make 1716 locks and give each pirate 924 keys. The method of distributing the keys is discussed in the proof.
Proof
Let \(N\) be the number of pirates, \(n\) be the number required to open the safe.
Any group of \(n-1\) pirate should together be unable to open some non-empty subset \(S\) of all the locks. If \(S\) was empty then they would be able to open all the locks with just \(n-1\) pirates.
We have that for each group of \(n-1\) pirates \(P\) there must be a distinct non-empty subset of locks \(S_P\) that cannot be opened by them. Furthermore, all subsets \(S_P\) must be disjoint. Therefore we need at least one lock for each group of \(n-1\) pirates, meaning at we require \(L \ge {N \choose n-1}\).
We will enumerate each group of \(n-1\) pirates and create a lock for each. Thus we have:
\[L = {N \choose n-1}\]Each pirate needs to be able to join any group of \(n-1\) pirates that he is not part of, and open their lock. Since these locks are distinct for each group, he needs to be able to open \(k \ge {N-1 \choose n-1}\) locks. If he has any less keys, there will be some groups who’s lock he wont be able to open. Thus we set the number of keys for each pirate to be:
\[k = {N-1 \choose n-1}\]Now for each lock you distribute the keys to all pirates, except the selection of \(n-1\) pirates corresponding to that lock. Consider a group of \(n-1\) pirates. There will be a single lock that they cannot open together. However, any pirate other than these \(n-1\) will be able to open that lock, thus any group of \(n\) pirates will be able to open all the locks.
For \(N=13\), \(n = \left\lceil \frac{N}{2} \right\rceil = 7\), we have that \(L = 1716\) locks and \(k = 924\) keys for each pirate.
Marble dropping
You are in a 100 story building and you have two identical marbles. You want to find out the highest floor in the building you can drop marbles off without them breaking. After you drop a marble, if it breaks it is unusable. If it survives it is not weakened at all.
Find the minimum number of drops you need to guarantee finding the highest floor you can safely drop marbles from.
You need at most 14 drops.
Proof
Let the maximum number of drops be \(d\). If we have 1 marble we can only test \(d\) floors by starting from the bottom and working our way up.
With 2 marbles, we know if we break the first marble on the first drop, we will only have 1 marble and \(d-1\) drops. Therefore our first drop should be floor \((d-1) + 1 = d\), since we can test the lower floors with one marble is required.
If the first drop succeeds we still have 2 marbles, but only \(d-1\) drops. Therefore if the second drop fails we can only test \(d-2\) floors with 1 marble. Thus we should go \(d-1\) floors above where we are, or floor number \(d + (d-1)\).
Continuing like this we can see that the maximum number of floors we can test is given by:
\[F_{max} = \sum_{i=1}^d i\]The smallest \(d\) such that we can test 100 floors is 14.
Drop the first marble on floors \([14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99]\) until it breaks. Then with the second marble, incrementally test the floors starting from one above the last good drop.
General case
With \(M\) marbles and \(D\) drops, the number of floors you can test is given by:
\[F(M,D) = \sum_{m=1}^{\min(M,D)} {D \choose m}\]Firstly note, having more than \(M > D\) is useless because even if a marble broke on every drop, we would only need \(M = D\) marbles. Thus we will restrict the number of marbles to \(M = \min(M, D)\) without loss of generality.
In any given strategy, decide how many marbles will break, and call it \(m\). If you know which drops those marbles broke on that is enough to tell you the floor number (given you know the strategy used to pick the floors).
There are \({D \choose m}\) different ways of choosing the positions where the marbles break. If we sum over all possible numbers of marbles broken it will give us the maximum number of different floors we can test with \(M\) marbles and \(D\) drops, with any strategy.
Any strategy that achieves this limit is thus optimal.
Let us define such a strategy. We will use the variables:
- \(d\) for the current number of drops left
- \(m\) for the current number of marbles left
- \(x_{max}\) for the maximum floor number we can safely drop a marble from.
- \(x\) for the current floor number
Initially set \(d=D\), \(m=M\), \(x_{max} = 0\) and \(x = 0\). Then proceed as follows:
- Set \(x = x_{max} + F(m-1, d-1) + 1\)
-
Drop a marble from from floor \(x\), and set \(d = d-1\)
- If it survives set \(x_{max} = x\)
- If it breaks set \(m = m - 1\)
- If \(d > 0\) and \(m > 0\) jump back to the top
- Otherwise stop, the maximum safe floor is \(x_{max}\)
Coin rotation
Take two equally sized coins and keep one fixed. Roll the other along the outside of the the first coin, without slipping, until it has gone all the way around the first coin. That is, the second coin rolls along a distance equal to its circumference.
How many rotations did the second coin make?
2 rotations!
Proof
The easiest way to see this is to first draw a line equal to the coins circumference. It will take the coin one rotation to roll along the length of the line. Now with the start of the line fixed and the coin fixed at the end of the line, curve the line into a circle. The coin will rotate one more during this process.
When the coin rolls along the outside of a circle, both these rotations happen at once: one from rolling and one from traveling along a curve.
Also see the Coin-rotation paradox. page on Wikipedia.
False Equations
Each of these proofs result in a false statement. Identify the mistakes.
\(2 = 1\)
Let \(a\) and \(b\) be non-zero numbers.
| \(a = b\) | |
| \(a^2 = a b\) | Multiply by \(a\) |
| \(a^2 - b^2 = ab - b^2\) | Subtract \(b^2\) |
| \((a-b) (a + b) = b (a - b)\) | Factor |
| \(a + b = b\) | Divide by \(a-b\) |
| \(2 b = b\) | Substitute \(a = b\) |
| \(2 = 1\) | Divide by \(b\) |
What went wrong?
You can’t divide through by \(a-b\). Since \(a = b\), this is dividing by 0.
\(4 = 5\)
| \(20 = 20\) | Start with a true equation |
| \(36 - 16 = 45 - 25\) | |
| \(16 - 36 = 25 - 45\) | Multiply by \(-1\) |
| \(16 - 36 + \frac{81}{4}= 25 - 45 + \frac{81}{4}\) | Add \(\frac{81}{4}\) to both sides |
| \(4^2- 36 + \left( \frac{9}{2} \right)^2 = 5^2 - 45 + \left( \frac{9}{2} \right)^2\) | |
| \(4^2 - \left( 2 \times4 \times \frac{9}{2} \right) + \left( \frac{9}{2} \right)^2 = 5^2 - \left( 2 \times 5 \times \frac{9}{2} \right) + \left( \frac{9}{2} \right)^2\) | Reduce 35 and 45 to factors |
| \(\left( 4 - \frac{9}{2} \right)^2 = \left( 5 - \frac{9}{2}\right )^2\) | Factorise |
| \(4 - \frac{9}{2} = 5 - \frac{9}{2}\) | Take the square root of both sides |
| \(4 = 5\) | Subtract \(\frac{9}{2}\) |
What happened?
Square roots have 2 solutions in general. When taking the square root in the proof, on one side we took the negative square root and on the other side we took the positive square root.
If on the other hand we took the positive square root on both sides we would have:
\[\begin{align} - \left(4 - \frac{9}{2}\right) & = 5 - \frac{9}{2} \\ \frac{1}{2} & = \frac{1}{2} \end{align}\]This is obviously true.
\(2 = 1\), the calculus way
We know from the power rule that: \(\frac{d}{dx} x^2 = 2 x\)
However, what if we re-write \(x^2\) as the sum of \(x\)s:
\[\begin{align} \frac{d}{dx} x^2 & = \frac{d}{dx} (x + x + x + \ldots + x) \\ & = \frac{d}{dx} x + \frac{d}{dx} x + \frac{d}{dx} x + \ldots + \frac{d}{dx} x \\ & = 1 + 1 + 1 + \ldots + 1 \\ & = x \end{align}\]Hence \(2x = x\) for any \(x\), therefore \(2 = 1\).
What’s going on here?
We can’t differentiate a sum whose number of terms is dependant on \(x\) by simply taking the sum of the derivatives. To make the fallacy here more explicit, write out the sum formally:
\[f(x) = x^2 = \sum_{i=0}^x x\]There are a few fallacies here. Firstly this equation is not meaningful for non-integers. Functions are only differentiable on a continuous space such as the real numbers.
For the second fallacy, note that in the proof, we took the derivative with respect to each term in the sum, but not with respect to the number of terms. The number of terms is a function of \(x\) and has to be taken into account.
Since the sum is a function of \(x\), we must use the chain rule when evaluating this. However this approach does not get us very far. Let the function that the sum denotes be called \(g(x)\). Unsurprisingly we find that \(g(x) = x^2\), leaving us with the same problem.
\(0 = 1\), integration by parts
Let us evaluate the indefinite integral: \(\int \frac{1}{x} dx\)
Let:
\[\begin{align} u &= \frac{1}{x} &dv &= dx &\\ du &= - \frac{1}{x^2} dx &v &= x& \end{align}\]Thus by integration by parts:
\[\begin{align} \int \frac{1}{x} dx & = \frac{x}{x} - \int \frac{1}{x^2}x dx \\ \int \frac{1}{x} dx & = 1 + \int \frac{1}{x} dx \\ 0 & = 1 \end{align}\]What happened?
This problem illustrates an improper application of integration by parts. When using the formula, a constant of integration \(C\) must be added. Up the second last line the equations are correct. However, the last line does not follow, as you cannot cancel \(\int \frac{1}{x}dx\), because they are not necessarily equal. There are an infinite number of antiderivatives of \(\frac{1}{x}\), which all differ by a constant factor.
In reality the last line should read:
\[0 = 1 + C\]Which is trivially true.
Too many solutions
A quadratic has either 0, 1, or 2 unique solutions. Look at this equation:
\[\frac{(x-a)(x-b)}{(c-a)(c-b)} + \frac{(x-b)(x-c)}{(a-b)(a-c)} + \frac{(x-c)(x-a)}{(b-a)(b-c)} = 1\]Without loss of generality we can assume \(a < b < c\). Now note that \(x = a\), \(x = b\) and \(x = c\) are all unique solutions.
How can this equation have 3 unique solutions?
The equation is not actually quadratic in \(x\). It doesn’t depend on \(x\) at all, and hence has an infinite number of solutions for \(x\).
Proof
The original equation:
\[\frac{(x-a)(x-b)}{(c-a)(c-b)} + \frac{(x-b)(x-c)}{(a-b)(a-c)} + \frac{(x-c)(x-a)}{(b-a)(b-c)} = 1\]Multiply by \((a-b)(b-c)(a-c)\):
\[(x-a)(x-b)(a-b) + (x-b)(x-c)(b-c) + (x-a)(x-c)(a-c) = (a-b)(b-c)(a-c)\]Expand:
\[(x^2 - (a + b) x + ab)(a-b) + (x^2 - (b + c) x + bc)(b-c) - (x^2 - (a + c) x + ac)(a-c) = (a-b)(b-c)(a-c)\]Collecting \(x\) terms:
\[x^2 (a - b + b - c - a + c) + x (a^2 - b^2 + b^2 - c^2 -a^2 + c^2) + ab(a-b) + bc(b-c) - ac(a-c) = (a-b)(b-c)(a-c)\]Thus all the \(x\) terms cancel out, leaving an equation that is always true.
Unequal equations
Take the following equation:
\[x^2 + x = -1\]\(x = 0\) is not a solution so therefore we can divide by \(x\) and rearrange:
\[\begin{align} x + 1 & = - \frac{1}{x} \notag \\ \frac{1}{x} + x & = -1 \end{align}\]Combining the equations:
\[\begin{align} x^2 + x & = \frac{1}{x} + x \\ x^2 & = \frac{1}{x} \\ x^3 & = 1 \\ x & = 1 \end{align}\]However, if we substitute into the original equation, we get:
\[1^2 + 1 = -1\]What happened?
The original quadratic has roots at:
\[x = \frac{-1 \pm \sqrt{3}}{2}\]However, when we combine the rearranged equations, we form a cubic equation. This adds a solutions, so now:
\[x = \frac{-1 \pm \sqrt{3}}{2}, 1\]And indeed, these are the three cube roots of one.
In general setting two equations equal to each other can generate more solutions, that don’t satisfy the original equations independently. This is because you are removing constraints, in this case, the constraint that both equations equaled \(-1\).
Missing square
The four coloured pieces in the image below can be put together in two different ways to make these shapes with base 13 units and height 5 units. Why is there one square missing in the second arrangement?
Neither of the \(13 \times 5\) “triangles” is a true triangle, because what appears to be the hypotenuse is bent. In the first “triangle” the hypotenuse bends inwards, and in the second it bends outwards.
Specifically, the blue triangle in the image has a slope of \(\frac{2}{5} = 0.4\) while the red triangle has a slope of \(\frac{3}{8} = 0.375\). This discrepancy accounts for the extra square.
All horses are the same color
We will prove that in any group of horses, all horses are the same color.
We will use induction to prove this claim. First, we establish a base case for one horse (\(n = 1\)). We then prove that if \(n\) horses have the same color, then \(n+1\) horses must also have the same color.
The base case, \(n=1\) is trivially true. In a group with one horse, all horses have the same color.
For the inductive case, assume that \(n\) horses always are the same color.
Consider a group consisting of \(n+1\) horses. First, exclude one horse and look only at the other \(n\) horses; all these are the same color, since this is given by the inductive case. Likewise, exclude some other horse (not identical to the one first removed) and look only at the other \(n\) horses. By the same reasoning, these, too, must also be of the same color. Since the first excluded horse is in the second set of \(n\) horses, it is the same color as the non-excluded horses and by the same logic so is the second excluded horse. Hence all \(n + 1\) horses are the same color.
This proves the inductive case that if any group of \(n\) horses are the same color, then so is any group of \(n+1\) horses.
Thus, in any group of horses, all horses must be the same color.
Where is the flaw in the logic?
The flaw is in assuming it is possible to find a horse who was not excluded by either of the groups of \(n\) in the inductive case.
For the two exluded horses to be the same color, there must be a third horse in the group to compare against.
Thus the induction fails for \(n=2\).
Disrupted scale
A scale balances a cup of water with a certain weight. Will the balance be upset if you put your finger in the water?
Yes.
The water imparts an upward force on your finger as you immerse it, so you must exert a downward force to overcome it. That force is transferred to the cup and then to the scale, which sinks.
Find the magnet
On a table are two iron rods - one blue, one red. One of them is magnetic and one of them is not, they are otherwise identical.
Determine which is the magnet without using any other tools.
Place the bars so they form a “T” with the blue magnet as the top. A magnet’s field is strong at its poles, but nearly non-existent in the middle. If the bars stick, the red bar is a magnet, otherwise it is the blue bar.
Plane on a conveyor belt
A plane is on an infinitely long conveyor belt. The conveyor belt runs backward at a speed equal to what the plane would be going if the conveyor belt was not there. The plane is on wheels which are working properly.
Can the plane take off?
Yes, the plane can take off.
Proof
The power for the engines come from the turbines, which is acting against the air. Thus the plane will develop a velocity relative to the air around it. With enough thrust it will gain enough speed relative to the air to take off.
The conveyor belt only acts on the wheels, making them rotate faster, but does not impede the motion of the plane.
Radioactive cookies
You have three cookies. One emits alpha radiation, one emits beta radiation and one emits gamma radiation. You have to eat one, put another in your pocket and put a third into a lead box. What do you do with each cookie?
- Put the beta emitting cookie in the lead box. That will protect you from that cookie.
- Put the alpha emitting cookie in your pocket. Alpha radiation is easily stopped by a piece of paper (or your pants).
- Eat the gamma cookie. Gamma radiation is the least ionizing of the three, so it is the least likely to do damage once inside your body. In addition, it is energetic enough that much of it is likely to escape your body without interacting with it.
Resistor network
Cube
Imagine a cube, where each edge is a \(1 \Omega\) resistor.
What is the effective resistance between opposite corners of the cube?
The effective resistance is \(\frac{5}{6} \Omega\) .
Proof
Let’s call one of the corners point \(A\) , through which we will force 1 A of current into the circuit. Call the opposite corner point \(B\) , through which we will draw 1 A of current from the circuit. Thus overall, 1 A is flowing from \(A\) to \(B\) . We will set the voltage at \(B\) to \(V_B = 0\) .
Now look at the 3 corners adjacent to \(A\) , call them \(A_1\) , \(A_2\) and \(A_3\) . By symmetry, the current through an edge between \(A\) and any \(A_i\) is:
\[I_A = \frac{1}{3} \text{ A}\]Thus the voltage drop \(V_1\) , between \(A\) and any point \(A_i\) is given by:
\[V_1 = I_A R = \frac{1}{3} \text{ V}\]Now look at the 3 corners adjacent to \(B\) , call them \(B_1\) , \(B_2\) and \(B_3\) . The situation is the same as above with the current flowing in the opposite direction, hence the voltage drop \(V_2\) between any point \(B_i\) and \(B\) is given by:
\[V_2 = \frac{1}{3} \text{ V}\]Now there are 6 equivalent ways for the current to flow in the middle resistor, between the points \(A_i\) and \(B_i\) . Thus the current flowing through each path is \(\frac{1}{6}\) A. The voltage drop \(V_3\) between any connected \(A_i\) and \(B_i\) is given by:
\[V_3 = \frac{1}{6} \text{ V}\]The total voltage drop between \(A\) and \(B\) can be found by following any path from \(A\) to \(B\) , thus:
\[V_A = V_B + V_2 + V_3 + V_1 = \frac{5}{6} \text{ V}\]Finally, use Ohm’s law to find the effective resistance:
\[R_{\text{eff}} = \frac{V}{I} = \frac{\left(\frac{5}{6}\right)}{1} = \frac{5}{6} \text{ } \Omega\]Infinite lattice
Imagine an infinitely extending 2D square lattice. Between any two adjacent intersection points is a resistor of \(1 \Omega\) .
What is the effective resistance between two adjacent intersection points?
The effective resistance is \(\frac{1}{2} \Omega\) .
Proof
Label the two adjacent points \(A\) and \(B\) . We will superimpose two ways of applying current to this circuit:
- Force 1 A into the circuit at point \(A\) while holding the voltage 0 at infinity. Since each path out of \(A\) is equivalent, the current from \(A\) to \(B\) must be \(I_1 = \frac{1}{4}\) A.
- Draw 1 A into the circuit at point \(B\) while holding the voltage 0 at infinity. Since each path out of \(A\) is equivalent, the current from \(A\) to \(B\) must be \(I_2 = \frac{1}{4}\) A.
Now we superimpose the two cases to get the situation where we have 1 A of current flowing from \(A\) to \(B\) , giving a current \(I = I_1 + I_2\) through the resistor:
\[I = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \text{ A}\]The voltage difference between \(A\) and \(B\) is, by Ohm’s law:
\[V = IR = 1 \times \frac{1}{2} = \frac{1}{2} \text{ V}\]But overall, 1 A of current is going from \(A\) to \(B\) , thus the effective resistance, by Ohm’s law is:
\[R_{\text{eff}} = \frac{V}{I} = \frac{\left(\frac{1}{2}\right)}{1} = \frac{1}{2} \text{ } \Omega\]Rock in a boat
You are in a boat, and the boat is in a pool. There is a rock in the boat. You throw the rock overboard, and it sinks to the bottom of the pool.
What happens to the water level?
The water level goes down.
Proof
The rock is currently displacing the amount of water equal to its mass. When it is dropped to the bottom, it is only displacing the amount of water equal to its volume.
It is more dense than water, so the amount of water displaced by its volume is less than the amount of water displaced by its mass.
Therefore less water is displaced after the rock is thrown overboard, and hence the water level goes down.
3-way shootout
You are in a shootout with two others. Unfortunately you are not a very good shot, only hitting what you are aiming for one-third of the time. The one of the others hits two-thirds of the time, and the last always hits.
To be fair, everyone agrees to fire in order with the worst shot (you) going first. You keep going around in the circle until only one is left standing.
What is your best strategy? Assume everyone is trying to maximise their chance at being the lone survivor, and none of you will ever give up.
Your best strategy is to shoot into the air the first round, then keep firing at the survivor in subsequent rounds.
Proof
Let’s call you person #1, #2 the next best shot, and #3 the person who always hits.
First note that if anyone other than #3 shoots, they must shoot #3. If they shoot the other person and kill them, then they will be in a duel with #3 with #3 going first. #3 wins this duel since #3 never misses.
Therefore it is in #3’s best interest to turn it into a duel as soon as possible, otherwise the other two are just shooting at #3. Thus if #3 survives to their turn then they must shoot. #3 would rather be in a shoot-out with the weaker shooter, hence they would shoot and kill #2.
Thus when it is #2’s turn they must shoot at #3 and hit to survive at all. From this we can tell that by the end of the first round, either #2 or #3 will have been shot.
Finally we look at #1. We’ve already established that if #1 shoots anyone, it must be #3. If #1 shoots and kills #3 then #1 will be in a duel with #2, with #2 going first. If #1 misses then they will be in a duel with the survivor of #2 and #3, with #1 going first.
The probability that #1 wins if they shoot and kill #3 is:
\[\begin{align} P(\text{#1 wins } \mid \text{ #1 hits #3}) & = P(\text{#1 wins } \mid \text{ #2 shoots first}) \\ & = P(\text{#2 misses}) P(\text{#1 hits}) \\ & \qquad + P(\text{#1 misses}) P(\text{#1 wins } \mid \text{ #2 shoots first}) \\ P(\text{#1 wins } \mid \text{ #2 shoots first}) & = \frac{1}{3} \left( \frac{1}{3} + \frac{2}{3} P(\text{#1 wins } \mid \text{ #2 shoots first}) \right) \\ P(\text{#1 wins } \mid \text{ #2 shoots first}) & = \frac{1}{7} \end{align}\]The probability that #1 wins if they shoot and miss #3 is:
\[\begin{align} P(\text{#1 wins } \mid \text{ #1 misses #3}) & = P(\text{#1 wins } \mid \text{ #2 hits #3}) + P(\text{#1 wins } \mid \text{ #2 misses #3}) \\ & = \frac{2}{3} P(\text{#1 wins against #2 } \mid \text{ #1 shoots first}) \\ & \qquad + \frac{1}{3} P(\text{#1 wins against #3 } \mid \text{ #1 shoots first}) \\ & = \frac{2}{3} \left( P(\text{#1 hits #2}) + P(\text{#1 misses #2}) P(\text{#1 wins } \mid \text{ #2 shoots first}) \right) \\ & \qquad + \frac{1}{3} P(\text{#1 hits #3}) \\ & = \frac{2}{3} \left( \frac{1}{3} + \frac{2}{3} \frac{1}{7} \right) + \frac{1}{3} \frac{1}{3} \\ & = \frac{2}{7} + \frac{1}{9} \\ & = \frac{25}{63} \end{align}\]Thus #1 has a higher chance of winning if they miss their shot!
Therefore you should intentionally miss the first shot by shooting into the air. After the first round, you will be in a duel with one of the other two people. You will win about 40% of the time.
General case for 3 people
Number the people #1, #2 and #3 such that the probability that a person hits their target is \(x_p\), with \(x_1 < x_2 < x_3\). Also, define \(\bar{x}_i = 1 - x_i\).
Define the probability \(P_{p_1, p_2, p_3}(p)\) that person \(p\) wins when the shooting order is \(p_1, p_2, p_3\) in the 3 person case.
Similarly, define \(P_{p_1, p_2}(p)\) for the 2 person case. For convenience let \(P_{p_1, p_2}(p) = 0\) if \(p \notin {p_1, p_2}\).
2 person case
We will do the 2 person case first, since the 3 person case reduces to this once a person is hit.
Each person can shoot at the other, or intentionally miss. Clearly, intentionally missing is bad because their opponent is always going to shoot at them: if their opponent hits they die; if their opponent misses they are back to where they started, but have given the opponent a free shot. Because the shooters must shoot, we can say for either person #\(i\):
\[\begin{align} P_{i,j}(i) & = x_i + \bar{x}_i P_{j,i}(i) \\ P_{j,i}(i) & = \bar{x}_j P_{i,j}(i) \end{align}\]Combining these equations we get:
\[\begin{align} P_{i,j}(i) & = x_i + \bar{x}_i \bar{x}_j P_{i,j}(i) \\ & = \frac{x_i}{1 - \bar{x}_i \bar{x}_j} \end{align}\]The probability that the other person #\(j\) wins when #\(i\) shoots first is just the complement:
\[P_{i,j}(j) = 1 - P_{i,j}(i)\]Simplifying:
\[\begin{align} P_{i,j}(j) & = 1 - \frac{x_i}{1 - \bar{x}_i \bar{x}_j} = \frac{1 - \bar{x}_i \bar{x}_j - x_i}{1 - \bar{x}_i \bar{x}_j} = \frac{\bar{x}_i - \bar{x}_i \bar{x}_j}{1 - \bar{x}_i \bar{x}_j} \\ & = \frac{\bar{x}_i x_j}{1 - \bar{x}_i \bar{x}_j} \end{align}\]Note that it is always better to start shooting first.
3 person case - Who shoots
Each person has three options, shoot either of the remaining people, or intentionally miss (shoot the air).
If person #\(i\) does shoot at a person then they are hoping to hit (otherwise they would shoot the air). If it hits then person #\(i\) will be in a duel with the survivor, where #\(i\) goes second. Thus they shoot #\(j\) instead of #\(k\) if:
\[\begin{align} P_{k,i}(i) & > P_{j,i}(i) \\ \frac{\bar{x}_k x_i}{1 - \bar{x}_k \bar{x}_i} & > \frac{\bar{x}_j x_i}{1 - \bar{x}_j \bar{x}_i} \\ x_i (\bar{x}_k - \bar{x}_k \bar{x}_j \bar{x}_i) & > x_i (\bar{x}_j - \bar{x}_j \bar{x}_k \bar{x}_i) \\ \bar{x}_k & > \bar{x}_j \\ x_k & < x_j \end{align}\]Hence, we have:
Lemma 1: If anyone shoots at another person, they will always shoot at the person with the higher accuracy.
If everyone shoots in the air then no one dies and the dispute is never resolved, in which case the probability of being the lone survivor for any of the people is 0. Thus at least one person shoots. Even in the case where shooting leads to certain death, this is the same as not resolving the dispute and hence we can assume either.
If one person is shooting then the other two can’t both be intentionally missing. In this case it is always better for the person that the shooter is shooting at to shoot back (assuming they haven’t been shot yet). Therefore we have:
Lemma 2: At least two people are shooting in any round where everyone survives.
#3 must either shoot #2 by Lemma 1 or shoot in the air.
- If #3 is shoots in the air then by Lemma 2 both #1 and #2 are shooting, and by Lemma 1 they are both shooting at #3. If they both miss, #3 is back to where they started and #3 shoots in the air again. The other two would continue shooting at #3 until they hit, giving #3 no chance of winning.
- If #3 shoots at #2 then #3’s chance of winning in this case is \(x_3 P_{1,3}(3) + \bar{x}_3 P_{1,2,3}(3) > 0\).
Thus #3 shoots at #2.
#2 must either shoot #3 by Lemma 1 or shoot in the air.
- If #2 shoots #3, they are hoping for a duel with #1. Since #1 would start the duel, the probability that #2 would win is \(P_{1,2}(2)\).
- If #2 shoots in the air, then #2’s best case scenario is that #3 will miss their shoot at #2 then #1 will hit #3. This results in a duel with #1 where #2 shoots first. Even allowing that #1 definitely hits, then the probability that #2 wins is \(\bar{x}_3 P_{2,1}(2)\).
#2 shoots at #3 if #2 would prefer hitting to missing:
\[\begin{align} P_{1,2}(2) & > \bar{x}_3 P_{2,1}(2) \\ \bar{x}_1 P_{2,1}(2) & > \bar{x}_3 P_{2,1}(2) \\ \bar{x}_1 & > \bar{x}_3 \\ x_1 & < x_3 \end{align}\]This is always true so #2 will shoot at #3.
#1 will either shoot #3 by Lemma 1 or shoot in the air.
-
If #1 shoots #3 they are hoping for a duel against #2 where #1 goes second. In this case #1 has a probability of winning of:
\[P_{2,1}(1) = \frac{\bar{x}_2 x_1}{1 - \bar{x}_2 \bar{x}_1}\] -
If #1 shoots the air, then the other two will shoot at each other. This will continue until either #2 or #3 is shot. In both cases #1 duels with the survivor, and gets to shoot first. The probability that #1 wins in this case is:
\[\begin{align} P_{1 \text{air}} & = x_2 P_{1,2}(1) + \bar{x}_2 (x_3 P_{1,3}(1) + \bar{x}_3 P_{1 \text{air}}) \\ & = x_2 P_{1,2}(1) + \bar{x}_2 x_3 P_{1,3}(1) + \bar{x}_2 \bar{x}_3 P_{1 \text{air}} \\ & = \frac{x_2 P_{1,2}(1) + \bar{x}_2 x_3 P_{1,3}(1)}{1 - \bar{x}_2 \bar{x}_3} \\ & = \frac{x_1}{1 - \bar{x}_2 \bar{x}_3} \left( \frac{x_2}{1 - \bar{x}_1 \bar{x}_2} + \frac{\bar{x}_2 x_3}{1 - \bar{x}_1 \bar{x}_3} \right) \end{align}\]
#1 will shoot at #3 if and only if #1 would prefer hitting to missing:
\[\begin{align} \frac{\bar{x}_2 x_1}{1 - \bar{x}_2 \bar{x}_1} & > \frac{x_1}{1 - \bar{x}_2 \bar{x}_3} \left( \frac{x_2}{1 - \bar{x}_1 \bar{x}_2} + \frac{\bar{x}_2 x_3}{1 - \bar{x}_1 \bar{x}_3} \right) \\ \bar{x}_2 (1 - \bar{x}_2 \bar{x}_3) (1- \bar{x}_1 \bar{x}_3) & > x_2 (1 - \bar{x}_1 \bar{x}_3) + \bar{x}_2 x_3 (1 - \bar{x}_1 \bar{x}_2) \end{align}\]Thus #1 will shoot at #3 when:
\[C > 0 \text{ where } C = \bar{x}_2 (1 - \bar{x}_1 \bar{x}_3) (1 - \bar{x}_2 \bar{x}_3) - x_2 (1 - \bar{x}_1 \bar{x}_3) - \bar{x}_2 x_3 (1 - \bar{x}_1 \bar{x}_2)\]3 person case - Probabilities
Let \(x'_1\) be the probability that #1 hits when there are 3 players. This is the same as \(x_1\) when #1 aims, but is \(0\) when #1 intentionally misses.
Then the probability that person #n wins is:
\[P_{1,2,3}(n) = x'_1 P_{2,1}(n) + \bar{x}'_1 (x_2 P_{1,2}(n) + \bar{x}_2 (x_3 P_{1,3}(n) + \bar{x}_3 P_{1,2,3}(n)))\]Which resolves to:
\[P_{1,2,3}(n) = \frac{x'_{1} P_{2,1}(n) + \bar{x}'_1 x_2 P_{1,2}(n) + \bar{x}'_1 \bar{x}_2 \bar{x}_3 P_{1,3}(n)} {1 - \bar{x}'_1 \bar{x}_2 \bar{x}_3}\] \[x'_1 = \begin{cases} x_1 & \text{ if } C > 0 \\ 0 & \text{ if } C \le 0 \end{cases} \text{ where } C = \bar{x}_2 (1 - \bar{x}_1 \bar{x}_3) (1 - \bar{x}_2 \bar{x}_3) - x_2 (1 - \bar{x}_1 \bar{x}_3) - \bar{x}_2 x_3 (1 - \bar{x}_1 \bar{x}_2)\]Original problem
For this problem we have:
\[(x_1, x_2, x_3) = \left(\frac{1}{3}, \frac{2}{3}, 1\right)\]From this we get \(C \approx -0.6 < 0\), hence #1 simply shoots the air. The probability #1 wins (which is true for any values where \(C < 0\)) is given by:
\[P_{1,2,3}(1) = \frac{x_1}{1 - \bar{x}_2 \bar{x}_3} \left( \frac{x_2}{1 - \bar{x}_1 \bar{x}_2} + \frac{x_3 \bar{x}_2}{1 - \bar{x}_1 \bar{x}_3} \right)\]Solving this with our values, we agree with our previous result:
\[P_{1,2,3}(1) = \frac{25}{63}\]Gender odds
In these questions assume that the boys and girls are equally likely to be born.
In a two-child family, one child is a boy. What is the probability that the other child is a girl?
The probability is \(\frac{2}{3}\)
Proof
There are 4 possible two-child families:
- Boy Boy
- Boy Girl
- Girl Boy
- Girl Girl
(4) is not possible, since we know that the family has a boy. There are 3 possibilities and in 2 of the the other child is a girl.
This gives a probability of \(\frac{2}{3}\).
The unintuitive result is because the probability of a family having both a boy and a girl is twice as likely as having 2 boys (or 2 girls).
In a two-child family, the older child is a boy. What is the probability that the other child is a girl?
The probability is \(\frac{1}{2}\)
Proof
List the 4 possible two-child families. The older child is listed first, then the younger.
- Boy Boy
- Boy Girl
- Girl Boy
- Girl Girl
This time only (1) and (2) are possible since we know that the older child is a boy. In only 1 of these 2 possibilities is the other child a girl.
This gives a probability of \(\frac{1}{2}\).
Gender ratio
There is a country where every family keeps having children until they have a boy. If they have a girl, they have another child. If they have a boy, they stop. Boys are girls are equally likely to be born.
What is the proportion of boys to girls in this country?
The ratio of boys to girls is 1:1.
Proof
Let’s assume for now that we don’t know the strategy that the families use to decide whether to have another child. However, the births are statistically independent.
For each birth in the country, we have a \(\frac{1}{2}\) chance of having a girl, and a \(\frac{1}{2}\) chance of having a boy. Thus after \(n\) births, we expect to have on average \(\frac{n}{2}\) girls and \(\frac{n}{2}\) boys.
This gives a ratio of 1:1. Further this is true regardless of what strategy the families use to decide when to have children.
In this specific case we can also determine the expected number of girls per family as:
\[E(g) = \frac{1}{2}(1 + \frac{1}{2}(1 + \frac{1}{2}( 1 + ... ))) = \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + ... = 1\]This represents that there is a 50% chance of having at least one girl. Given one girl, there is a 50% chance of having at least 2 girls, and so on. Since each family stops at one boy, there is on average 1 boy and 1 girl in each family.
Guess the larger number
I pick two distinct real numbers at random from some arbitrary distribution. Then I flip a coin and if it comes up heads, I tell you the larger one, if it comes up tails I tell you the smaller one. You must guess whether it was the larger one or the smaller one.
Give a strategy that wins with a probability greater than \(\frac{1}{2}\).
If you see an \(x\), guess “larger” with probability \(p(x)\) and “smaller” with probability \(1-p(x)\), where \(p(x)\) is a monotonically increasing function from \(\mathbb{R}\) to \((0,1)\) . A possible function is:
\[p(x) = \frac{1}{2} + \frac{\arctan(x)}{\pi}\]Proof
Suppose the distinct numbers are \(a\) and \(b\) with \(a < b\) .
The probability, \(P\), of guessing correctly is:
\[\begin{align} P & = \frac{1}{2}(1 - p(a)) + \frac{1}{2}p(b) \\ & = \frac{1}{2} + \frac{1}{2} (p(b) - p(a)) \end{align}\]From this we can see that:
\[P > \frac{1}{2} \text{ if } p(b) > p(a)\]But since \(p(x)\) is monotonically increasing and \(b > a\), we have \(p(b) > p(a)\). Thus the overall probability of winning is greater than \(\frac{1}{2}\).
Monty hall
You are on a game show with your host Monty Hall. You are shown 3 doors. Two of the doors have a goat behind them, and the remaining door has a car behind it.
You are asked to choose a door, but not open it. The host Monty, knowing where the car is, then opens one of the other doors and shows that it has a goat behind it. There are now two closed doors, the one you chose and the remaining door. You are asked if you wish to stay with your original door, or switch.
To maximise your chance of winning the car, do you switch or stay?
Always switch.
Proof
We can assume that we always pick the first door without loss of generality (because each door has a \(\frac{1}{3}\) chance of having the car).
After we pick the door, these are 6 possible (equally likely) arrangements:
C - -
C - -
- C -
- C -
- - C
- - C
Where C stands for car, and - stands for the goat.
After Monty opens one of the door we didn’t pick, and shows nothing. If there is a goat behind the first door then Monty has no choice about which door to open. Thus we have:
C X -
C - X
- C X
- C X
- X C
- X C
Where X represents an open door.
We can see that in 4 of the 6 cases, it is better to switch. This means that if we switch we have a \(\frac{2}{3}\) chance of winning the car.
Amnesiac Monty
Suppose now that Monty forgot where the car was. After you picked your door Monty guessed randomly and opened one of the doors. It opens up to show a goat. Relieved, Monty asks you whether you want to switch doors to the unopened door.
Is it better to switch or stay?
This time it doesn’t make a difference! Both doors have a 50% chance of having the car.
Proof
As before, we can assume that we always pick the first door without loss of generality (because each door has a \(\frac{1}{3}\) chance of having the car).
After we pick the door, these are 6 possible (equally likely) arrangements:
C - -
C - -
- C -
- C -
- - C
- - C
Where C stands for car, and - stands for the goat.
After Monty opens one of the door we didn’t pick. However this time, the choice is random so there is a possibility that Monty reveals the car:
C X -
C - X
- X - (Car is revealed!)
- C X
- X C
- - X (Car is revealed!)
Where X represents an open door.
We know we aren’t in the 2 cases where the car is revealed, so there are 4 possible scenarios we can be in. In 2 of these 4 cases it is better to switch giving a \(\frac{1}{2}\) chance of winning the car.
Commentry
This is a well-known problem. See the Wikipedia page for a deeper discussion and more variants.
⇪Prisoners' names in boxes
There are 100 prisoners. Inside a room there are 100 boxes each holding the name of a different prisoners. One at a time, each prisoner is lead into the room. They are allowed to open 50 boxes in any order, and look inside. They are allowed to base their decision for what boxes to open based on what they have already seen. If they find the box containing their name, they are lead out and the boxes are returned to their original state.
The prisoners are allowed to go free if all 100 prisoners find the box containing their own name. They are not allowed to communicate with the other prisoners after the first prisoner has been lead into the room.
Find a strategy that wins at least 30% of the time.
First, number each prisoner from 1 to 100. When a prisoner goes into the room they:
- Looks in the box corresponding to their number.
- If they don’t find their name they looks in the box corresponding to the name of the prisoner in the box they just opened.
- They continue until they find their name, or they cannot open any more boxes.
This strategy results in a ~31.2% chance of winning.
Proof
Let us generalise the problem to \(N\) prisoners, where each prisoner is allowed to open \(n = \lceil c N \rceil\) boxes, where \(\frac{1}{2} \le c \le 1\).
In the strategy given, a given prisoner succeeds if they are part of a cycle of at most \(n\) in the permutation of names. For all prisoners to succeed there must be no cycles of size greater than \(n\). We can also see that if there is a cycle of size greater than \(n\), then it is the only such cycle because \(\frac{1}{2} \le \frac{n}{N} \le 1\).
We first find the probability, \(P_L(k)\), that there is some cycle of length \(k\) for some \(k > n\):
- A cycle of length \(k\) occurs on \(k\) of the \(N\) elements, so there are \({N \choose k} = \frac{N!}{k!(N-k)!}\) possibilities for this.
- Within a cycle there are \((k-1)!\) ways to arrange the elements.
- Outside the cycle there are \(N-k\) elements that can be arranged in \((N-k)!\) ways.
- In total there are \(N!\) arrangements.
Thus we have:
\[\begin{align} P_L(k) & = \frac{\frac{N!}{k!(N-k)!} (k-1)! (N-k)!}{N!} \\ & = \frac{(k-1)!}{k!} \\ & = \frac{1}{k} \end{align}\]Therefore the probability, \(P\), that the strategy succeeds is:
\[\begin{align} P & = 1 - \sum_{k=n+1}^N P_L(k) \notag \\ & = 1 - \sum_{k=n+1}^N \frac{1}{k} \\ & = 1 - H_N + H_n \notag \\ & \text{where } H_i = \sum_{k=1}^i \frac{1}{k} \text{ is the nth Harmonic number} \notag \end{align}\]For \(N = 100\) and \(n = 50\) we get \(P \approx 0.3118\).
Large \(N\)
Let \(P(N)\) be the probability that our strategy succeeds with \(N\) prisoners, where each prisoner is allowed to choose \(n = \lceil c N \rceil\) boxes, where \(\frac{1}{2} \le c \le 1\).
We have from the equation above that:
\[P(N) = 1 - \sum_{k=n+1}^N \frac{1}{k}\]As \(N \rightarrow \infty\) we have:
\[\begin{align} \lim_{N \rightarrow \infty} P(N) & = 1 - \int_{n}^N \frac{1}{k} dp \\ & = 1 - \left[ \log k \right]_{n}^N \\ & = 1 - \log N - \log n \\ & = 1 - \log \frac{N}{n} \\ & = 1 + \log c \end{align}\]For \(c = \frac{1}{2}\) we have \(P \approx 0.3069\).
All values of \(0 \le c \le 1\)
If we generalise the problem, we require more than a unique cycle \(n = \lceil c N \rceil\) for our solution to fail.
Let us find the probability \(P_l(k)\), that a given box is part of a cycle of length \(k\). We see that:
- A cycle of length \(k\) occurs on \(k\) of the \(N\) elements. One element is chosen for us so, there are \({N - 1 \choose k - 1} = \frac{(N-1)!}{(k-1)!(N-k)!}\) possibilities for this.
- Within a cycle there are \((k-1)!\) ways to arrange the elements.
- Outside the cycle there are \(N-k\) elements that can be arranged in \((N-k)!\) ways.
- In total there are \(N!\) arrangements.
Thus we have:
\[\begin{align} P_l(k) & = \frac{\frac{(N-1)!}{(k-1)!(N-k)!} (k-1)! (N-k)!}{N!} \\ & = \frac{(N-1)!}{N!} \\ & = \frac{1}{N} \end{align}\]Let \(P_l = \frac{1}{N}\). We require that the probability of there being no cycles of length \(k > n\).
Let the probability \(P_L(k, N)\) be the probability that the longest cycle is of length \(k\) in a problem of size \(N\).
We start by looking at the first element. It has a \(P_l\) chance of being in a loop of length \(1\), in which case the probability the longest cycle is be of length \(k\) will be \(P_L(k, N-1)\).
Likewise it has a \(P_l\) chance of being in a loop of length 2, in which case the probability the longest cycle is be of length \(k\) will be \(P_L(k, N-2)\).
In general it has a \(P_l\) chance of being in a loop of length \(i\), in which case the probability the longest cycle is be of length \(k\) will be \(P_L(k, N-i)\), for \(i \le k\) or 0 for \(i > k\). Thus we have:
\[P_L(k, N) = \sum_{i=1}^k \frac{1}{N} P_L(k, N-i)\]Let \(P(N)\) be the probability that the longest cycle in a problem of size \(N\) is \(n\):
\[P(N) = \frac{1}{N} \sum_{i=1}^{n} P(N-i)\]Prisoners with hats in a circle
Three prisoners are standing in a circle. They are blindfolded and either a red or blue hat is placed randomly on the head of each prisoner. When the blindfold is removed they can see the colour of the hats on the other two prisoners but not their own. They cannot communicate in any way.
They are each given a piece of paper on which they must write “red”, “blue” or “abstain”. They are allowed to go free if at least one prisoners guesses their hat colour correctly, and none guess incorrectly.
The prisoners find out about this the day before and attempt to find a strategy over night. What is the strategy which maximises their probability of going free?
All three prisoners follow the same rule:
- If the other two prisoners have matching hat, guess the opposite colour.
- If the other two prisoners have different colour hats, abstain.
This results in a 75% chance of victory.
Proof
If all 3 hats are the same, all 3 prisoners will guess wrong. This happens with probability \(\frac{2}{8}\). If there are 2 hats the same, and 1 different then one prisoner will guess right, and the others will abstain. This will happen with probability \(\frac{6}{8} = 75\%\).
For every possible arrangement where a prisoner \(P_i\) guesses right, there must be an arrangement where prisoner \(P_i\) guesses wrong. By having all prisoners be wrong in the same arrangement, we can cover many different arrangements where only one person guesses, and is correct.
Extension
This problem can be generalised to the case where there are \(2^k - 1\) prisoners, where \(k\) is positive integer. To do this we use the Hamming code.
We can represent the prisoners as bits, with (red, blue) being equivalent to (0, 1). For a problem of size \(2^k - 1\) We can obtain the code Hamming\((2^k - 1, 2^k - k -1)\). Let us refer to those arrangements which represent valid strings under the Hamming code as “good” arrangements.
Our strategy for each prisoner is to check if they looks like they are in a “good” arrangement. If they are, then they write down the opposite of what the arrangement says. Otherwise, they abstain.
We can see that in a “good” arrangement, everyone guesses wrong. This happens in \(2^{2^k-k-1}\) arrangements.
However, in all other arrangements, exactly one person writes down their hat colour (correctly), and all the others abstain. This is because the Hamming code corrects for one bit errors. This happens in \(2^{2^{k}-1} - 2^{2^k-k-1}\) arrangements.
This is optimal since when we are wrong, all prisoners are wrong together. However, when we are right, only one prisoner votes.
The probability that we are right, \(P\), can be given by the number of arrangements in which we are right, over the total number of arrangements:
\[\begin{align} P & = \frac{2^{2^{k}-1} - 2^{2^k-k-1}}{2^{2^{k}-1}} \\ & = 1 - \frac{1}{2^{k}} \end{align}\]We can see that as the number of prisoners grows we get higher chances of winning.
Random number bluff
There is a die that, when rolled, gives a random real number between 0 and 1. We play the following game:
- Player 1 rolls the die
- Player 1 may either tell Player 2 the number, or lie and report any number between 0 and 1
- Player 2 can either roll the die to try and beat the number they were told, or accuse Player 1 of lying
- Player 2 wins if they beat the number they were told, or they accuse Player 1 of lying and is right
- Player 1 wins otherwise
What’s the best strategy for Player 1?
The best strategy for Player 1 to tell the truth if they roll higher than \(\frac{1}{e}\), or otherwise lie, reporting in the range \(\left[\frac{1}{e}, 1\right]\) according to the probability density function:
\[p(x) = e \left( \frac{1}{x} - 1 \right)\]Proof
Suppose Player 1 has chosen a strategy, and has reported a value in the range \([x, x+dx]\). This is referred to as the range “near” \(x\) .
If Player 2 chooses to trust, then they will win with probability:
\[P_{trust} = 1 - x\]If Player 2 chooses to accuse, then their probability of winning depends on how often Player 1 lies “near” \(x\). Let \(L(x) dx\) be the probability that Player 1 lies and reports a value in the range \([x, x+dx]\). The probability that the roll really was in the range \([x, x+dx]\) is \(dx\). Therefore, Player 2 will win when accusing with probability:
\[\begin{align} P_{accuse} & = \frac{L(x) dx}{L(x) dx + dx} \\ & = 1 - \frac{1}{L(x) + 1} \end{align}\]Player 2 should only accuse if:
\[\begin{align} P_{accuse} & > P_{trust} \\ 1 - \frac{1}{L(x) + 1} & > 1 - x \\ L(x) & > \frac{1}{x} - 1 \end{align}\]Now if Player 1 ever wants to report “near” \(x\) they should make sure that there are enough lies “near” \(x\) so that Player 2 is indifferent to trusting and accusing:
- If Player 1 doesn’t lie “near” \(x\) often enough, then Player 2’s best choice will be to trust. Knowing this, Player 1 can lie a little more often “near” \(x\) rather than reporting “near” \(y\) for any \(y<x\).
- If Player 1 lies too much “near” \(x\) , then Player 2’s best choice will be to accuse. Knowing this, Player 1 can lie a little less often “near” \(x\) and instead report “near” \(z\) for the largest \(z\) that doesn’t get lied “near” often enough (even if \(z < x\)).
Therefore, for any \(x\), Player 1’s best strategy will involve either never reporting “near” \(x\), or lying “near” \(x\) with probability:
\[L(x) = \frac{1}{x} - 1\]We can see that this means that \(P_{accuse} = P_{trust}\), and thus Player 2 will be indifferent to trusting or accusing. Thus we can assume that Player 2 will trust.
Given that Player 2 will trust always in this strategy, Player 1 should report high values as often as possible, and never report low values. Thus values less that some \(N\) will never be reported, and values greater than \(N\) will be lied “near” with a probability \(L(x)\).
We require that the probability of lying for \(x > N\) be the same as the probability for rolling \(x < N\):
\[\begin{align} N & = \int_N^1 \left( \frac{1}{x} - 1 \right) dx \\ & = \left[ \log x - x \right]_N^1 \\ & = \log 1 - 1 - \log N + N \\ \log N & = -1 \\ N & = \frac{1}{e} \end{align}\]Now we require that for rolls where \(x < N\), Player 1 will lie, reporting “near” \(y\) with probability \(cL(y)\), and that the sum of all probabilities of \(y\) in the range \([N, 1] = 1\):
\[\begin{align} \int_N^1 c L(x) dx & = 1 \\ c \int_N^1 \left( \frac{1}{x} - 1 \right) dx & = 1 \\ c \frac{1}{e} &= 1 \\ c & = e \end{align}\]Giving the required probability distribution in the equation: \(p(x) = e \left( \frac{1}{x} - 1 \right)\)
Red marbles, blue marbles
You have two jars, 50 red marbles and 50 blue marbles. You need to place all the marbles into the jars such that when pick a random marble out of a random jar, you maximize the chances that it will be red. You can arrange the marbles however you like, but each marble must be in a jar.
How many of each type of marble do you put in each jar?
Put 1 red marble in one jar, and put all the other marbles in the other jar.
Proof
For each jar we have the chance that we get a red marble will be \(\frac{\text{# red marbles in jar}}{\text{# total marbles in jar}}\) . We can maximise our chance of getting red marble in one jar by making all the marbles in that jar red.
However we would like as many marbles as possible in the other jar to have a high chance of getting red in that one also. The minimum number of marbles we can use is 1, hence we put a single marble in the first jar.
By putting the rest of the marbles in the second jar we get nearly a 75% chance of picking a red marble. Suppose we have \(n \ge 1\) of each type of marble, then the probability of finding a red marble will be:
\[\begin{align} P & = \frac{1}{2}\left(1\right) + \frac{1}{2}\left(\frac{n-1}{n+(n-1)}\right) \\ & = \frac{1}{2}\left(\frac{2 n - 1 + n -1}{2 n - 1}\right) \\ & = \frac{1}{2}\left(\frac{3 n - 2}{2 n - 1}\right) \end{align}\]For our problem we have \(n = 50\) , \(P = 0.7475\) .
Note that as \(n\) goes to \(\infty\) we have:
\[\lim_{n \rightarrow \infty} P = \frac{3}{4}\]Thus for any \(n\) we can’t get better than \(\frac{3}{4}\) chance.
Seats on a plane
There is a fully booked flight, which has just begun boarding passengers. Each passenger has already been assigned a seat. The first passenger to board is distracted and does not look at their assigned seat, but sits down in a random seat. For the other passengers, when they board, if their assigned seat is free they sit there. Otherwise they sit at a random seat that is free.
What is the probability that the last passenger to board sits in their assigned seat?
The last passenger has a 50% chance of finding their seat free.
Proof
From the point of view of the last passenger, it is an equivalent problem if the previous passengers all kick the distracted passenger out of the seat if it belongs to them. In this situation the distracted passenger chooses a different free seat.
They continue being dislodged until they ends up in either their own seat, or the seat of the last passenger. Both of these situations are equally likely, and hence the last passenger has a 50% chance of finding their seat free.
Tallest in line
11 people are standing facing forward in a line. On average, how many people will be taller than everyone in front of them?
On average about 3 people will be taller than everyone in front of them.
Proof
Let \(E(n)\) be the expected number of people who are taller than the people in front for a line of \(n\) people.
Suppose we add a person of random height to the end of the line of length \(n-1\), so the length is now \(n\). This does not affect what any of the existing people in the line see. The person added sees everyone, and thus must be the tallest overall to be taller than everyone in front. There is a \(\frac{1}{n}\) chance that this person is the tallest out of the group of \(n\) random people. Hence:
\[E(n) = E(n-1) + \frac{1}{n}\]In an empty line 0 people are taller than anyone so \(E(0) = 0\). Hence:
\(E(n) = \sum_1^n \frac{1}{n} = H_n\) where \(H_n\) is the nth harmonic number.
For our problem, \(E(11) \approx 3.02\).
10x10 tiling
Suppose there is a 10x10 grid.

Can you tile it completely with 1x4 tiles (oriented in any direction)?

No, it is impossible.
Proof
Label the grid cells with letters A-D as follows, filling in each diagonal line with each successive label:

Note that anywhere you place a 1x4 tile, it will cover one of each label A-D. Thus each letter will be covered the same number of times.
However, the grid has an unequal count of each letter. Note that each row has either two or three of each letter. Looking at just the letters A and B:
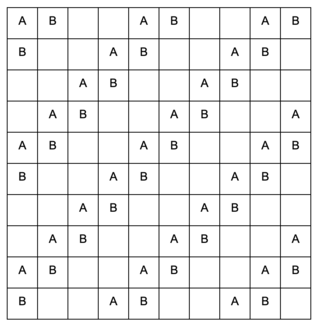
There are 5 rows with 3 As, but 6 rows with 3 Bs. Hence there is one more B than As in the grid. Thus any tiling that covers every A will leave a B uncovered.
Broken chessboard
Dominoes
You have a chessboard with two squares removed.

You also have an infinite supply of the dominoes.

Can you cover the entire chessboard with dominoes, with none overlapping, and none going outside the bounds of the board?
It is not possible.
Proof
First colour the chessboard in the normal checkered pattern.

We know that a domino must cover both a black and a white square. However, both the squares missing are black. This means that no matter how you lay the dominoes there will always be two uncovered white squares, which cannot be paired with a black one.
Tetraminos
You have a chessboard with four squares removed.

You also have an infinite supply of the tetraminos.

Can you cover the entire chessboard with tetraminos, with none overlapping, and none going outside the bounds of the board?
It is not possible.
Proof
First colour the chessboard and the tetraminos in the normal checkered pattern.

There are two possible patterns for the tetraminos.
We will put the tetramino such that its colours match with the colour of the squares it is covering. Each of the first kind of tetramino adds three black squares and only one white square. Each of the second kind of tetramino adds three white squares and only one black square.
There’s an equal number of black and white squares, so there must be equally many of both kinds of tetraminos. But there are only \(15 \times 4\) squares left, so there can’t be equal numbers of each kind.
Cutout shapes
Square
Divide a square int into four identical squares. Remove the bottom right hand square.
Divide the resulting shape into four identical shapes.
Triangle
Divide an equilateral into four identical shapes. Remove the bottom right hand shape.
Divide the resulting shape into four identical shapes.
Note that in both the square and triangle case, we can divide the remaining 3 shapes again into 4 parts. We need to pick 3 of the smaller parts to make the new identical shape. If we pick the part from each of the 3 shapes that are next to each other, we automatically get the required shape.
Cutting a square
You have a \(5 \times 5\) piece of paper. Two diagonally opposite corners of this paper are truncated:
You also have scissors. Show how to cut up the \(5 \times 5\) paper into two pieces, so that the two pieces can then be interlocked to form a \(6 \times 4\) rectangle.
The cut required is shown in red:
Dividing cakes
Mary baked a rectangular cake. John secretly carved out a small rectangular piece, ate it and got away. The remaining cake has to be split evenly between Mary’s two kids. The cake is layered, and the kids want to be sure they both get the same amount of each layer.
How could this be done with only one cut through the cake?
Make a vertical cut that goes through the midpoints of the original cake, and the midpoint of the missing section.
Proof
Cutting a rectangle through its midpoint will always divide it in half. Thus each half in our divided cake will have half of the original cake with half of the missing section.
This makes the size of each slice exactly equal.
Nine dots
Can you connect all nine dots using 4 continuous straight lines?

The required lines are shown in red:
Quarantine squares
Can you draw 2 squares such that the nine dots are separated into their own regions?

Join the midpoints of the outer square’s edges to create a square at a 45 degree angle. Then join the midpoints of the edges of that square to create a small square in the center.
Rows of trees
Can you plant 9 trees such there are 10 rows of 3 trees?
An example solution:
To construct:
- Start with a middle row of 3 equally spaced trees.
- Place a center tree in the top row at any distance from the center.
- Place a center tree in the bottom row at the same distance from the center as the top.
- The positions of the remaining trees are forced by extending the top and bottom rows parallel with the center row.
Bat and ball
A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball.
How much does the ball cost?
The ball costs 5c.
Proof
Let the cost of the ball in dollars be \(x\). Then:
\[\begin{align} x + (1+x) & = 1.10 \\ 2 x + 1 & = 1.10 \\ 2 x & = 0.10 \\ x & = 0.05 \\ \end{align}\]Commentry
This is a classic problem because the intuitive answer when hearing the problem is 10c until you stop and calculate it.
Dried potatoes
You have a 100 kg bag of potatoes. The potatoes are 99% water. You leave the potatoes out overnight and they dry out so they only contain 98% water.
How much do the potatoes weigh now?
50 kg.
Proof
Being 99% water, the potatoes are originally 99 kg water and 1 kg solid. When dried, the solid weight remains the same, but is now 2% of the weight. Thus 1 kg is now 2% \(= \frac{1}{50}\)th of the weight, giving a total weight of 50 kg.
Lily pads
In the middle of a pond is a single lily pad. Each day the number of lily pads doubles. After exactly 14 days the lily pads cover the pond completely.
After how many days did the lily pads cover half the pond?
After 13 days the lily pads covered half the pond.
Since the lily pads doubles each day, on the next day the pads will double to cover the whole pond, as required.
Magic square
Enter the numbers 1 to 9 into a 3x3 grid such that every row, column and diagonal with 3 cells adds up to 15.
Each number can only be used once.
Up to rotations and reflections, the grid must be filled in like this:
Construction
There are 8 ways to use the numbers 1-9 to add to 15:
- 1+5+9
- 1+6+8
- 2+4+9
- 2+5+8
- 2+6+7
- 3+4+8
- 3+5+7
- 4+5+6
This lines up with the 8 different 3 cell lines we need to fill in, so each sum must be used once. Count the how many times each number appears in a sum - this constraints where it can appear in the grid:
| Number | Count |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 3 |
| 7 | 2 |
| 8 | 4 |
| 9 | 2 |
From this we can tell that:
- 5 is the only number that appears 4 times, so it must be in the center.
- The remaining odd numbers appear 2 times each, so they must be in the middle of the edges. Place 1 and 9 opposite each other, then 3 and 7 in the remaining spots. This is symmetric up to rotations and reflections.
- All the even numbers appear 3 times, so they must be in the corners. Their positions are forced by the numbers that are already filled in. e.g. 2 must be adjacent to the 7 and the 9.
Squashed bee
Two trains enter a tunnel 200 km long at the same time from opposite directions. They are both travelling at 100 km/h.
As soon as they enter the tunnel a supersonic bee flying at 1000 km/h starts from one train and heads toward the other one. As soon as it reaches the other one it turns around and heads back toward the first. It keeps going back and forth between the trains until the trains collide in a fiery explosion in the middle of the tunnel.
How far did the bee travel? Assume the bee can turn instantaneously.
The bee travels 1000 km.
Proof
We don’t need to calculate the bees back-and-forth path, which would involve calculating an infinite sum. Instead we can consider the bees journey as a whole.
Let the length of the tunnel be \(L\), the speed of the trains be \(v_t\), and the speed of the bee be \(v_b\). Also set \(t = 0\) when the trains enter the tunnel.
The trains collide at the middle of the tunnel after traveling a distance of \(\frac{L}{2}\). When this happens the time is:
\[t = \frac{\left(\frac{L}{2}\right)}{v_t} = \frac{L}{2 v_t}\]During this time the bee has a constant speed of \(v_b\). Thus it travels a distance:
\[d = v_b t = \frac{L v_b}{2 v_t}\]For this problem, \(v_b = 1000\) km/h, \(v_t = 100\) km/h and \(L = 200\) km giving \(d = 1000\) km.
100 prisoners in a line
A group of 100 prisoners are told that the next day, they will be lined up single file, all facing forward. Hats of either red or blue colour will be randomly placed on their heads. Starting from the back each prisoner will be asked the colour of his hat. If the prisoner answers correctly, that prisoner will be released. The prisoners are allowed to come up with a plan overnight.
What is the best plan that will save the most number of prisoners?
The prisoner at the back will guess red if they sees an even number of red hats in front of them, or blue if they sees an odd number of red has in front of them. When the other prisoners are asked their colour, they add together the number of red hats the sees with the number of times they hear someone say red behind them. If it is even they say red, if it is odd, they say blue.
Proof
This works because the last prisoner makes known the parity of red hats for all the prisoners in front, and then the prisoners can update the parity based on what each subsequent prisoners says.
This saves the 99 people in the front with certainty, and the last prisoner with 50% chance. We can’t do any better than chance for the last prisoner as they have no information about their hat color.
Bad processors
You are an astronaut, and you have \(n\) computer processors. The processors have been exposed to cosmic radiation, but a majority of them are still good. Your goal is to find one good processor.
Each processor can be used to test another. The tester processor will tell you whether the other one is good or bad. Good processors always respond accurately. Bad processors respond randomly.
Determine a strategy for finding one good processor with certainty that uses no more than \(n-2\) tests in the worst case.
First, if \(n\) is even, throw one processor out. Now start a stack of processors, initially, it is empty. Now:
- If the stack is currently empty, pick a processor from the remaining processors and push it onto the stack.
-
If the stack is not empty, pick a processor and use it to test the processor on the top of the stack.
- If the testing processor reports that the top of the stack is bad, then throw both the testing and tested processors.
- If the testing processor reports that the top of the stack is good, the push it onto the stack so it becomes the new top.
- If the number of processors in in the stack is greater than the number of processors in the remaining pile, stop. The processor at the bottom of the stack is good.
- Otherwise repeat from the top.
Proof of correctness
If \(n\) is even there are at least 2 more good processors than bad processors, so throwing out a processor keeps the majority. Now we can assume the number of processors is odd.
Note that when processor reports that another processor is bad, at least one of the tester or the tested must be bad. This is because two good processors will never report bad when testing each other. Hence if we throw out the tester and the tested processors on every test that reports bad we preserve the fact that the good processors are in majority. Thus:
Lemma 1: The number of good processors in the stack and remaining piles combined always outnumber the bad.
Because we start out with an odd number of processors, and we only throw out processors 2 at a time, we have:
Lemma 2: The number of processors in the stack and remaining pile combined is always odd.
Every iteration we always remove one processor from the remaining pile. Therefore, unless both the stack and the remaining pile have zero processors, the remaining pile will eventually have less processors than the stack. However, by Lemma 2 we have that the number of processors in the stack and remaining pile combined can never be zero (as zero is not an odd number). Thus:
Lemma 3: Our strategy always terminates.
Now every processor in the stack reported that the one before it was good. This can only happen if the stack has zero or more good processors at the bottom, followed by zero or more bad processors. There can be no good processors on top of bad processors, otherwise the they would have reported bad when testing.
Lemma 4: If our stack contains any good processors, then they located in a contiguous chain at the bottom of the stack.
If the number of processors in the stack is greater than the number of processors in the remaining pile then:
- By Lemma 1 there must be at least one good processor in the stack.
- By Lemma 4 the processor at the bottom of the stack must be good.
- By Lemma 3 our strategy is guaranteed to terminate.
Thus our strategy always finds a good processor.
Proof of runtime
We know that the first processor never does any testing, because it is added to the chain straight away.
Furthermore the last remaining processor never does any testing:
- If the stack is empty, then it is added to the stack without being tested.
- The stack cannot have just one processor, or the total number of processors would be 2, violating Lemma 2.
- If the stack has more than 1 processor, then our strategy has already terminated, without the last processor being tested.
Each processor only performs a test when it is removed from the remaining pile. Thus each processor performs a maximum of one test each. Because the first and the last processors never perform any tests, we have that the maximum number of tests performed is \(n-2\).
Bridge crossing
Four people come to a river in the night. There is a narrow bridge, but it can only hold two people at a time. They have one torch and, because it’s night, the torch has to be used when crossing the bridge. Person \(A\) can cross the bridge in one minute, \(B\) in two minutes, \(C\) in five minutes, and \(D\) in eight minutes. When two people cross the bridge together, they must move at the slower person’s pace.
Can they all get across the bridge in 15 minutes or less?
First note that making the fastest person the torch-bearer and having them shuttle the others across takes 17 minutes, and thus isn’t sufficient. The time can be improved by sending the two slowest people over the bridge at the same time.
| Elapsed time | Left side | Right side | |
|---|---|---|---|
| 0 | A B C D |
Initial position | |
| 2 | C D |
A B |
A and B cross |
| 3 | A C D |
B |
A returns |
| 11 | A |
B C D |
C and D cross |
| 13 | A B |
C D |
B returns |
| 15 | A B C D |
A and B cross |
Catch the fugative
A police officer is chasing a fugative. The fugative comes to a row of 17 houses and hides in the backyard of one of the houses.
The police officer knows the the fugative is cornered into this row of houses and can check one house at a time. If the officer checks the house where the fugative is hidding the fugative will be caught. Otherwise the officer can check another house but during this time the fugative can jump to either of the neighboring houses. The fugative can’t stay in the same location otherwise they may be caught by the owner of the house.
How can the officer catch the fugative?
Start by searching the 2nd house. Then search each house in order up to the 16th house. Then do the same in reverse, searching from the 16th house down to the 2nd house (i.e. the 16th house gets searched twice in a row).
By the end the fugative would have been found.
Proof
First note that the fugative alternates odd and even houses because they always move to an adjacent house. This is also true for the officer for each of the two passes. Thus on each pass the officer and fugative maintain the same parity difference.
Suppose the fugative starts on an even numbered house. On the first pass the officer starts at the 2nd house, hence when the officer is searching an even house the fugative is at an even house, and similarly, when the officer is searching an odd house the fugative is at an odd house. As the officer moves along the street, the fugative can never get to the other side of the officer as the fugative can never be on either of the houses adjacent to the officer. Thus the officer will eventually find the fugative on the first pass if the fugative starts on an even numbered house.
If the fugative is not found on the first pass, then when the officer searches the 16th house for the first time the fugative must be at an odd numbered house. When the officer then searches the 16th house again for the second pass the fugative must have moved to an even numbered house.
Now on the second pass the same logic applies, except we know that the fugative starts on an even numbered house. Hence the officer catches the fugative by the time the officer reaches the 2nd house.
Table of coins
Your friend wants to play a game with you. You sit down with them at a round table. They produce a large pile of coins.
“Ok”, your friend says, “We’ll take turns putting coins down, no overlapping allowed, and the coins must rest on the table surface. The first person who can’t put a coin down loses.”
Your friend wants to go first.
Is this game fair?
No, the game isn’t fair. The first player always has a winning strategy.
Proof
The following is the winning strategy for the first player:
Put the first coin exactly in the center.
Next, for each coin player #2 puts down, place one directly opposite it. That is, place it so that the center of the table is exactly half way between the two coins.
This will generate a completely symmetric layout of coins on the table. Whenever the player #2 selects a free space to place a coin in, the space opposite is guaranteed to be free as well. Since player #1 is always guaranteed an open
Crashing engines
Two engines are designed to be parachuted to the random points of the infinite straight railway. After landing, they face in the same direction on the track (either forwards or backwards).
The engines operate automatically by the on-board computer with a single absolutely identical program inside each computer.
The engines both discard their parachutes at the point of landing, and then their control programs start.
The computer can recognize the following 4 commands:
FORWARD- Move one step forward.BACKWARD- Move one step backward.GOTO <label>- Switch control to the command marked by<label>(each command may have a unique label).IF (CHUTE) THEN <command>- If there is a parachute at that point, execute<command>(any command described above). The engines cannot recognize if the parachute is their own.
You are the programmer of the engine on-board computer. Your goal is to make two engines crash. Can you do that?
Use the following program:
go:
FORWARD
IF(CHUTE) THEN GOTO run
BACKWARD
FORWARD
GOTO go
run:
FORWARD
GOTO run
Proof
First note that the engines always travel forwards overall. Since they are both
facing the same direction they will continue going forward (in the go
loop) at the same speed until the one who is following finds the parachute of
the other. It will then start moving at a faster speed than the first (in the
run loop), as it no longer has to do a BACKWARD FORWARD every
iteration. Thus it will eventually catch the first.
Hidden salaries
Three co-workers would like to know their average salary. They trust each other to be honest, however they do not want to disclose their actual salaries to anyone else.
Determine a strategy so that they can find the average.
First number the three people, #1, #2 and #3. Let the salary of person \(i\) be \(s_i\). Also, make each person come up with a random number \(r_i\).
Then use the following strategy:
- #1 writes the value \((s_1 + r_1)\) on a piece of paper and hands it to #2.
- #2 adds the value \((s_2 + r_2)\) to the value they see on the paper that #1 gave. They write this new value \((s_1 + s_2 + r_1 + r_2)\) on a new piece of paper and hand it to #3.
- #3 adds the value \((s_3 + r_3)\) to the value they see on the paper that #2 gave. They write this new value \((s_1 + s_2 + s_3 + r_1 + r_2 + r_3)\) on a new piece of paper and hand it to #1.
- #1 subtracts \(r_1\) from the value they see on the paper that #3 gave. They write this new value \((s_1 + s_2 + s_3 + r_2 + r_3)\) on a new piece of paper and hand it to #2.
- #2 subtracts \(r_2\) from the value they see on the paper that #1 gave.= They write this new value \((s_1 + s_2 + s_3 + r_3)\) on a new piece of paper and hands it to #3.
- #3 subtracts \(r_3\) from the value he sees on the paper that #2 gave. They then divide the result by 3 to obtain the average \(\frac{s_1 + s_2 + s_3}{3}\), which they tell everyone.
Locking boxes
Alice wants to send an item to Bob, but unfortunately any items sent tend to get stolen unless they are in a locked box.
Alice and Bob both have padlocks, but they don’t have each others keys. How can Alice send the item to Bob?
- Alice puts the item in a box and locks it with her padlock.
- She then sends the box to Bob.
- Bob puts his own padlock on the box and sends it back to Alice.
- Alice removes her padlock and sends the box back to Bob.
- Bob removes his padlock and opens the box.
This strategy is used by Key Exchange algorithms to allow two parties to communicate securely without having to share a secret key.
Note that it assumes that Alice and Bob can recognise each others padlocks. Otherwise, an attacker could intercept the box and add their own padlock, instead of Bob’s and Alice would not know. Even if Alice and Bob could communicate, the attacker could send a copy of the box to Bob, and both Alice and Bob would think everything was fine.
Missing number
You have a list of 99 numbers, each of which is a number between 1 and 100. The numbers are not in order, but there are no duplicates. How do you find the missing number?
Add all the numbers, then subtract the total from 5050 (the sum of the numbers from 1 to 100). The result is the missing number.
Poisoned wine bottles
A king has 1000 bottles of wine, and is to serve 999 of them at a banquet in 24 hours. The problem is that 1 of the bottles is poisoned, and he has to figure out which it is before the banquet. He has 10 servants willing to sacrifice their lives to test the bottles. The poison takes 24 hours to take effect, so the king has only one shot at a test to single out the poisoned bottle. The poison is very strong and even when diluted will still kill within the time period.
How can he use his ten servants to find the single poisoned bottle out of 1000 bottles?
Number the bottles 0 to 999. Number the servants 0 to 9. Each servant drinks from bottles whose number has its \(i\)th bit set to 1.
After waiting for 24 hours, see which servants have died. Discard the bottle whose \(i\)th bit is 1 if the \(i\)th servant died, but 0 otherwise. This uniquely identifies the bottle.
In general this can be done for \(n\) bottles as long as the king has at least \(\lceil \log_2 n \rceil\) servants.
Prisoners and a lightbulb
A new prison has been built. It holds exactly 100 prisoners. Each prisoner is held in a solitary room with no way of communicating with the other prisoners, or anyone on the outside. At his leisure, the warden selects one prisoner at random, and escorts the selected prisoner to a central room for one hour. There is nothing in the central room except a light switch that controls a light bulb installed in the ceiling, which is visible but out of reach. While a prisoner is in the central room, they are allowed to turn the light switch on or off. They can also decide to tell the warden that they are certain that all 100 prisoners have been in the room.
If they are correct then everyone will be set free, but if they are not correct, then everyone will be executed. So, it is essential that they only talk to the warden when they are positive that they are correct.
All 100 prisoners are allowed to gather together before they are put in prison to discuss their strategy for getting out.
Known state, known time
The light is off before the first prisoner goes in. The prisoners are told that the warden will bring in one prisoner a day to the room. Can you come up with a plan that guarantees success (eventually)?
- Every prisoner starts off with a count of 1.
- Designate one prisoner as the “collector”.
- If the light is off when a prisoner enters the room, and their count is 1, they turn the light on and decrease their count.
- If the light is on when the collector enters the room, they turn the light off and increase their count.
- When the collector’s count reaches 100, they notify the warden.
Proof and runtime
Every prisoner turns on the light at most once. The light is initially off, so when the collector has seen the light come on 99 times they knows that all other prisoners have been in the room. At this point the collectors count will be 100 and they alert the warden.
The probability \(p\) for a previously uncounted prisoner to arrive between the collectors visits (given \(n\) prisoners and \(x\) uncounted prisoners) is:
\[\begin{align} p = & 0 \times \text{probability the collector arrives } + \\ & 1 \times \text{probability an uncounted prisoner arrives } + \\ & p \times \text{probability a counted prisoner arrives } \\ = & 0\frac{1}{n} + 1\frac{x}{n} + p\frac{n-x-1}{n} \\ np = & x + p(n - x - 1) \\ p = & \frac{x}{x+1} \end{align}\]The expected time between visits for the collector is \(n\) days. Thus the expected time taken for a collector to see the light turn on is:
\[n\frac{x+1}{x}\]Thus the expected time for the prisoners to escape is:
\[n \sum_{x=1}^{n-1} \frac{x+1}{x}\]When \(n = 100\) this evalutes to about 10418 days, or about 28.5 years.
Note that this is not optimal. There are trivial improvements to this algorithm such as dynamically choosing the collector. For example, selecting the prisoner brought in on the second day, they can immediately count the prisoner on the first day and shorten their stay by an average of \(n\) days.
Unknown state, unknown time
Is it still possible to solve the problem if the prisoners do not know the initial state of the lightbulb or how often a prisoner will be brought to the room?
The algorithm for a known state already works if the prisoners don’t know how often they are brought to the room, so we just need to deal with the unknown state.
- Every prisoner starts off with a count of 1.
- Designate one prisoner as the “collector”.
- If the light is off when a prisoner enters the room, and their count is 1, and they have previously observed the light in both states (on and off), they turn the light on and decrease their count.
- If the light is on when the collector enters the room, and they didn’t turn it on, and it is not their first time in the room, they turn the light off and increase their count. In all other cases they toggle the light switch.
- When the collector’s count reaches 100, they notify the warden.
Proof
As with the algorithm for a known state, every prisoner turns on the light at most once.
The collector is always the first prisoner to change the initial state of the light switch. When a prisoner has seen the light in the both states, they can be sure that the collector has started counting. Hence, when a prisoner turns on the light the collector will count it.
If no other prisoners are turning on the light, the collector is toggling the light on and off between visits. This ensures that eventually all prisoners will see the lightbulb in both states.
Note that this solutions here is not optimal, it is a simple example of feasibility.
Multiple states
Suppose the lightbulb is replaced with a switch with multiple states, can the prisoners use that to escape faster?
Let \(n\) be the number of prisoners. The previous algorithms can be easily adjusted to take advantage of multiple states with the following differences:
- The collector resets the state to 0 (in the unknown initial state problem they toggle between 0 and the maximum value).
- Prisoners increment the state unless it is already at its maximum value.
- The collector increments their count by the value they see.
This will reduce the expected runtime by a factor equal to the number of switch states, when there are up to \(n - 1\) states.
If there are \(n\) or more states the first time a prisoner visits the room they update the switch from \(x\) to \(x + 1 \mod n\). The first prisoner to see the switch set to \(x \mod n\) (where \(x\) is the value they first saw) can alert the warden that all prisoners have visited the room.
This works even when the initial state and time between visits is unknown. The expected runtime for this is:
\[\sum_{x=1}^{n} \frac{n}{x} = nH_n \text{ where } H_n \text{ is the nth harmonic number }\]For \(n = 100\) this is about \(519\) days.
As with the previous algorithms, this solution is not optimal.
Prisoners' chessboard
Two prisoners are offered a chance to go free. One of the prisoners will be presented with a standard chessboard with 64 squares, but on each square is a coin. The coins are randomly facing heads and tails.
The guard chooses a square on the board, which we’ll call the Magic Square, and tells it to the first prisoner. The prisoner is then allowed to flip exactly one coin (from heads to tails or vice versa).
Then the second prisoner is shown the chessboard. To secure their freedom, the second prisoner must identify the location of the Magic Square, just by looking at the coins.
The prisoners may discuss any strategy beforehand. Can the prisoners go free?
This can be solved for any board with \(2^k\) squares. For a chessboard \(k = 6\).
Index the squares \(0, 1, \ldots, 2^k - 1\) and let:
\[\begin{align} S_i = & \begin{cases} 0 \text{ if square } i \text{ is tails before the flip} \\ 1 \text{ if square } i \text{ is heads before the flip} \end{cases} \\ S_i^\prime = & \begin{cases} 0 \text{ if square } i \text{ is tails after the flip} \\ 1 \text{ if square } i \text{ is heads after the flip} \end{cases} \\ \end{align}\]Determine the xor sum of the squares whose coins show heads:
\[a = \bigoplus \left( i S_i \right)\]Let the index of the Magic Square be \(m\). Flip the coin of the square \(m \oplus a\). The magic square can be determined as the xor sum of all the squares which show heads:
\[m = \bigoplus \left( i S_i^\prime \right)\]Proof
Let the index of the square flipped be \(r\):
\[r = m \oplus \bigoplus \left( i S_i \right)\]Given this, \(S_i\) can be defined as:
\[S_i^\prime = \begin{cases} S_i & \text{ if } i \ne r \\ 0 & \text{ if } i = r \wedge S_r = 1 \\ 1 & \text{ if } i = r \wedge S_r = 0 \\ \end{cases}\]The using the properties of xor:
\[\begin{align} m = & r \oplus \bigoplus \left( i S_i \right) \\ = & r \oplus r S_r \oplus \bigoplus_{i \ne r} \left( i S_i \right) \\ = & r S_r^\prime \oplus \bigoplus_{i \ne r} \left( i S_i^\prime \right) \\ = & \bigoplus \left( i S_i^\prime \right) \end{align}\]This is the same as the equation to determine the square, thus we correctly find the magic square.
Alternative proof
Let \(n\) be the number of squares and define \(k\) such that \(n = 2^k\). We will create \(k\) sets \(C_i \mid 0 < i \le k\) where:
\[C_i = \left\{ j \mid \text{ the } i \text{th bit in } j \text{ is set } \wedge 0 \le j < n \right\}\]We can see by construction that each square is in a unique subset of sets \(C_i\), and thus can be identified by which sets it is a member of. This can be seen by the fact that the set membership can be read off the binary representation of the square’s index.
Define the parity of \(C_i\) as the parity of the the number of heads in \(C_i\). Then the initial calculation (\(a = \bigoplus \left( i S_i \right)\)) calculates the parity of \(C_i\) as the \(i\)th bit of the result \(a\).
We wish to change the parity of the sets \(C_i\) so that they reflect the parity of the bits in \(m\). That is we want to flip a coin that is in all sets \(\left\{ C_i \mid \text{ parity } C_i \ne i \text{th bit of } m \right\}\). This is exactly what \(m \oplus a\) calculates.
Now the bits of \(m\) can be read off as the parity of the sets \(C_i\).
Boards with \(n \ne 2^k\) squares
If \(n\) is not a power of 2 then there is no possible solution. Note that there are \(2^n\) possible board states and we want to transmit one of \(n\) value. Each board state has \(n\) adjacent states it can transition to with the flip of a coin (one for each coin we can flip).
For any mapping there must exist a value which maps to at most \(\left\lfloor \frac{2^n}{n} \right\rfloor\) states by the pigeon-hole principle. This value can be adjacent to at most \(n \left\lfloor \frac{2^n}{n} \right\rfloor\) states.
\(n \left\lfloor \frac{2^n}{n} \right\rfloor < 2^n\) unless \(n | 2^n\). \(n | 2^n\) is only true when \(n\) is a power of 2. Thus if \(n \ne 2^k\) a solution is not possible because in any given strategy there will be some values which can’t be reached from all states.
River crossings
There is a river, with a boat on one side. The boat is only big enough for two people, or one person and an object. It requires an adult to row it.
In all scenarios the travellers start on the left bank of the river.
The farmer
A farmer comes to the river, with a wolf, a goat and a bail of hay. The wolf cannot be left alone with the goat, or else it will eat the goat. Likewise the goat will eat the hay if left alone with it.
How does the farmer get everything across the river?
Let:
Fstand for the farmerWstand for the wolfGstand for the goatHstand for the hay
The side with the boat is surrounded with brackets.
| Left bank | Right bank | |
|---|---|---|
(F W G H) |
Initial position | |
(F W H) |
G |
Farmer takes the goat across and comes back |
(F G H) |
W |
Farmer takes the wolf across and brings the goat back |
(F G) |
W H |
Farmer takes the hay across and comes back |
(F W G H) |
Farmer takes the goat across |
The criminals
Three thieves with three assassins come to the river. The theives refuse to be outnumbered by assassins at any point.
How can they all get across the river?
Let:
Tstand for a thiefAstand for an assassin
The side with the boat is surrounded with brackets.
| Left bank | Right bank | |
|---|---|---|
(A A A T T T) |
Initial position | |
(A A T T T) |
A |
An thief goes across with an assassin and comes back |
(A T T T) |
A A |
Two assassins go across and one comes back |
A T |
( T T A A) |
Two thieves go across |
(A A T T) |
T A |
A thief goes back with a assassin |
A A |
( T T T A) |
Two thieves go across |
A |
( T T T A A) |
An assassin goes back and two come across |
( T T T A A A) |
An assassin goes back and two come across |
The jealous couple
A jealous couple, a father and mother, are out with their son, dog and four four friends (two female and two male) when they come across a river. The man cannot be alone with either of the female friends, and the woman with either of the male friends. Finally, the dog will bite anyone who is with it, unless the son is there to control it. The dog can be left tied up alone.
How can the group cross the river?
Let:
Fstand for the fatherMstand for the motherWstand for a female friend (woman)Gstand for a male friend (guy)Sstand for the sonCstand for the dog (canine)
The side with the boat is surrounded with brackets.
| Left bank | Right bank | |
|---|---|---|
(F M W W G G S C) |
- |
Initial position |
(F M W W G G S) |
C |
The son takes the dog across and comes back |
(F M W W G S C) |
G |
The son takes a male friend across and brings the dog back |
(F M W W S C) |
G G |
The father takes a male friend across and comes back |
(M W W S C) |
F G G |
The mother takes the father across and comes back |
(F M W W) |
G G S C |
The son takes the dog across, but the father comes back |
(M W W) |
F G G S C |
The mother takes the father across and comes back |
W |
( F M W G G S C) |
The mother takes a female friend across |
C |
( F M W W G G S) |
The son takes the dog back and comes across with a female friend |
- |
( F M W W G G S C) |
The son goes back and comes across with the dog |
Shuffling people
You have an empty room, and a group of people waiting outside the room. At each step, you may either get one person into the room, or get one out. Can you make subsequent steps, so that every possible combination of people is achieved exactly once?
We will generate an algorithm by induction.
The base case is trivial, we start with an empty room and then let the one person in. This covers both possible states.
Now, assume that we have a solution for \(n\) people. We will show that we can construct a solution for \(n+1\) people. Note that the solution for \(n\) people also works in reverse, because the change will still be .
- We start by running the solution for \(n\) people - this covers all combinations which exclude the last person.
- Now we let the last person in and then run the solution for \(n\) people in reverse - this covers all combinations which include the last person.
At the end of the process, the last person will be the only one in the room.
This is known as a Gray code.
Sink the sub
An enemy submarine is on some unknown integer on the number line. It is moving at some unknown rate of \(v\) units per minute, where \(v\) is an integer.
You can launch a torpedo each minute at any integer on the number line. If the submarine is there, you hit it and it sinks. You have all the time and torpedoes that you want. You must sink the sub.
Devise a strategy that is guaranteed to eventually hit the enemy sub.
Look the grid of integer points on the Cartesian plane. Starting at \((0,0)\), visit each point in turn one every minute. Fire at \(f(t) = x + y t\) . This will guarantee to eventually hit the sub.
Proof
Let the sub’s position be given by \(s(t) = x_0 + v t\) . Note that both \(x_0\) and \(v\) are the set of integers ( \(\mathbb{Z}\) ). Since \(\mathbb{Z}\) is countable, we know that the set of all trajectories is countable also, as it is of size \(\mathbb{Z}^2\) .
Thus if we enumerate all possible trajectories and try each on in turn, we will eventually hit the sub.
In fact, this works if the sub can move to any rational number, algebraic number or any other countable set.
Spider's web
A fly is caught in a spider’s web and the spider is trying to catch it.

The fly and the spider start on the pictured intersections and take turns moving. During its turn the creature can move along an edge to a connected intersection - it must move, it can’t stay still.
How can the spider catch the fly if it has to move first?
Color the intersections as follows so that every move alternates between red and blue nodes, apart from the top node:
In the starting position, both the spider and the fly are on the same color. As long as the spider and fly stay on the red and blue nodes, they will always be on the same color after they both move. In this case the spider can’t catch the fly because the spider will always be forced to move to a node of the opposite color to the fly on its turn.
The only way to change this is to move up to the top green node. Once at the green node the spider can move so that it is on the same color as the fly after the spider’s move. The spider has changed the relative parity of their positions.
After this it can corner the fly by moving towards the fly’s position. The fly can’t get past the spider, because the spider controls of all the nodes around it. Since these controlled nodes are now the same color that the fly wants to move into, it controls the fly’s mobility.
Once in a corner, the fly has no choice but to move to a node where the spider can move to and catch it.
This is a type of Pursuit-evasion problem.
Bob and his brother
You are to meet with two brothers. You know that one of them, named Bob, has a very important package for you. Unfortunately, you never saw Bob or his brother, and don’t know who is who.
To make the matter worse, one of the brothers is a pathological liar who never tells the truth, while the other never lies. You do not know whether Bob is the liar or not.
Upon meeting the brothers, you can ask one short question of either of the brothers (but not both) to establish with certainty which of the two is Bob.
What question do you ask?
Ask “Is Bob a liar?” Only Bob will answer “No”.
Proof
There are four possibilities:
- You speak to Bob and he tells the truth: “No”.
- You speak to Bob and he lies: “No”.
- You speak to his brother and he tells the truth: “Yes”.
- You speak to his brother and he lies: “Yes”.
So it can be seen that Bob will always answer “No” and his brother will always answer “Yes”.
Knights and knaves
You are visiting an island where everyone is either a knight or a knave. Knights always tell the truth and knaves always lie. They can only answer yes-no questions.
Single inhabitant
You come across a lone inhabitant. How can you tell if they are a knight or a knave?
Ask a question to which you both know the answer. For example, “Are you a mushroom?”
“We are both knaves”
You come across two inhabitants. One tells you “We are both knaves”.
Are they knights or knaves?
They can’t both be knaves, otherwise the inhabitant would have lied about it. Hence the statement was a lie, and the speaker was a knave. This means the other must be a knight.
Same or different
You come across two inhabitants. The first claims they are both of the same type (both knights or both knaves), the second says they are different.
What are they?
Since the statements are different their types must be different, hence the second person is speaking the truth and is a knight. The first must therefore be a knave.
Village of knights and knaves
You come across a village with 10 people. 5 are knight and 5 are knaves. Knight always tell the truth and knaves always lie. All the villagers know each other and know who are knights and who are knaves. They will only answer yes-no questions.
What is the minimum number of questions you need to tell who is a knight and who is a knave.
You need 8 questions.
Proof
There are \(\binom{10}5 = 252\) possible combinations you need to disambiguate. This requires a minimum of \(\lceil log_2(252) \rceil = 8\) questions.
One strategy for this is to first identify one of the villagers. Ask one of the villagers a question with a known answer (e.g. “Are you a mushroom?”) to determine if they are a knight or a knave. We will now be able to reliably determine the truth based on their answers - if they are a knave we just need to invert their responses.
This leaves us with 7 questions to disambiguate the remaining \(\binom{9}{5} = 126\) combinations, which is less than \(2^7 = 128\) hence is still possible.
You thus use the identified villager to binary search through the possible combinations.
Shaded stones
An honest person has three stones, one white, one grey and one black.
They secretly chooses one stone, and allows you to ask one question, to which they will answer “Yes”, “No” or “I don’t know”.
Can you determine which stone the person chose?
Ask “If I chose a stone out of the two that you didn’t pick, would it be darker than yours?”
- If they have a black stone, they answer “No”.
- If they have a white stones, they answer “Yes”.
- If they have a grey stone, they must say “I don’t know”.
Honest and deceitful gods
You are on the road to heaven and you reach a fork in the road. One of the paths leads to heaven, however the other path leads to hell. At the fork there are two gods, one who always tells the truth, and one who always lies. You are allowed to ask one question to one of the gods.
What question do you ask to determine the path to heaven?
Ask one of the gods “If I were to ask the other god which path leads to heaven, what would he say?” Then take the opposite path.
Proof
First let us consider the question “Which path leads to heaven?”
To this the truthful god will point to the path to heaven, and the lying god will point to the path that leads to hell.
Now if we look at the question given in the solution, the truthful god will answer honestly and point to the path to hell (which is what the lying god would say leads to heaven). The lying god will also point to the path that leads to hell, because the it is the opposite of the path that the truthful god would say leads to heaven.
Thus whoever you ask, they will point to path that leads to hell. We simply pick the other path.