You are dropped on the surface of a very large planet, which has a single river which runs perfectly straight around the equator. You begin to explore the planet, in your dune buggy, by driving in a straight line away from the river, but a tornado hits you spinning you around and knocking you unconscious.
When you awake, you’ve forgotten which direction you had been travelling in. You do know however that you travelled 1000 km. You have an accurate compass and odometer on board. The river is in a canyon, and you can’t see it until you reach it.
You have enough fuel to go 6400 km. Can you make it back to the river (any point on the river)?
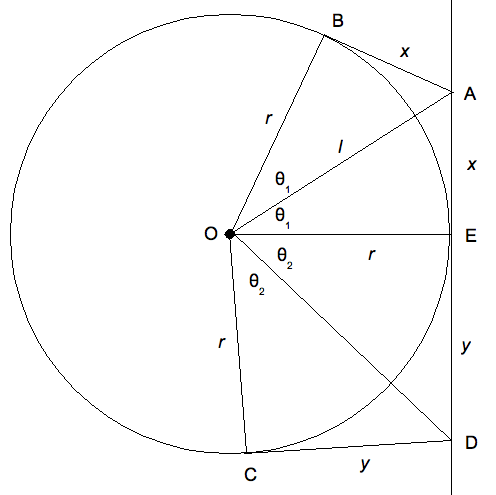
From point \(O\) travel:
- 1155 km to point \(A\)
- 577 km to point \(B\)
- 3665 km around the radius of the circle to point \(C\)
- 1000 km to point \(D\)
This will guarantee to come across the river.
Proof
Let the distance to the river be \(r\). The problem is equivalent to finding a curve that intersects with all of the tangents of a circle of radius \(r\).
To minimise the distance travelled we want to:
- Go directly to some tangent line (all are equivalent by symmetry)
- Follow it until we reach the circle
- Follow the circle around for some distance
- Then go to the closest point on our original tangent.
We will pick some arbitrary tangent, as all are equivalent. We choose the vertical tangent on the right side.
We need to head to some point \(A\) on the tangent, which we will say is an \(\theta_1\) from the horizontal. The length of the line from \(O\) to \(A\) is given by:
\[l = \frac{r}{\cos \theta_1}\]Next we travel from \(A\) to be \(B\), and this distance is given by:
\[x = r \tan \theta_1\]Next we travel around the circle from \(B\) to \(C\). This covers and angle of \(2 \pi - 2 \theta_1 - 2 \theta_2\). This gives adds a distance of:
\[a = 2 (\pi - \theta_1 - \theta_2) r\]Finally, to head from point \(C\) to point \(D\):
\[x = r \tan \theta_2\]This gives a total distance of:
\[\begin{align} d & = l + x + c + y \notag \\ & = r \left( \frac{1}{\cos \theta_1} + 2 (\pi - \theta_1 - \theta_2) + \tan \theta_1 + \tan \theta_2 \right) \end{align}\]We wish to minimise \(d\) thus we require that both of the following hold:
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = 0 \\ \frac{\partial d}{\partial \theta_2} & = 0 \end{align}\]Solving for \(\theta_1\):
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = r \left( \frac{\sin \theta_1}{\sin^2 \theta_1} - 2 + (1 + \tan^2 \theta_1) \right) \\ 0 & = \frac{\sin \theta_1}{\sin^2 \theta_1} + \tan^2 \theta_1 -1 \\ & = -\frac{2 \sin \theta_1-1}{\sin \theta_1-1} \\ & = 2 \sin \theta_1-1 \text{ where } \sin \theta_1 \ne 1 \\ \sin \theta_1 & = \frac{1}{2} \\ \theta_1 & = \frac{\pi}{6} \end{align}\]Solving for \(\theta_2\):
\[\begin{align} \frac{\partial d}{\partial \theta_1} & = r \left(- 2 + (1 + \tan^2 \theta_2) \right) \\ 0 & = \tan^2 \theta_2 - 1 \\ \tan \theta_2 & = 1 \\ \theta_2 & = \frac{\pi}{4} \end{align}\]Substituting \(\theta_1\) and \(\theta_2\) into the equation for \(d\):
\[\begin{align} d & = r \left( \frac{2}{\sqrt{3}} + \frac{7 \pi}{6} + 1 + \frac{1}{\sqrt{3}} \right) \\ & = r \left( \sqrt{3} + 1 + \frac{7 \pi}{6} \right) \end{align}\]For our problem, \(r = 1000\) this gives a total distance of:
\[d \approx 6397 \text{ km}\]