A rope with zero elasticity is placed tautly around the Earth’s equator.
Assume the Earth is a perfect sphere of radius 6378km.
Rope ring
How much longer would the rope need to be so that it can be form a ring 1m above the ground everywhere.
\(2 \pi \approx 6.28\) meters of rope is required.
Proof
Let \(c\) be the original length of rope, \(r\) the radius of the earth.
\[c = 2 \pi r\]Let \(\Delta c\) and \(\Delta r\) be the added rope and radius respectively.
\[\begin{align} c + \Delta c & = 2 \pi (r + \Delta r) \\ 2 \pi r + \Delta c & = 2 \pi r + 2 \pi \Delta r \\ \Delta c & = 2 \pi \Delta r \end{align}\]Thus the change in the length of rope is \(2 \pi \Delta r\) regardless of the original radius! In our problem \(\Delta r = 1\) m.
Pulled rope
Suppose instead we only want to pull the rope taut so that it was 1m high at one point. How much rope is required for this?
Adding 0.75 mm is sufficient to lift the rope up 1m!
Proof
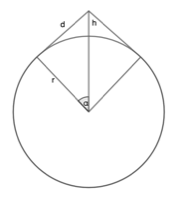
The length of the rope can be given by \(2 (\pi - \alpha) r + 2d\), thus the extra rope required is:
\(\Delta c = 2 (\pi - \alpha) r + 2d - 2 \pi r = 2 d - 2 \alpha r\) where \(\alpha = \arctan\left(\frac{d}{r}\right)\)
We can calculate \(d\) using Pythagoras’ forumla:
\[d^2 + r^2 = (r+h)^2\] \[d = \sqrt{2rh + h^2}\]Combining:
\[\Delta c = 2 \sqrt{2rh + h^2} - 2 r \arctan\left(\frac{\sqrt{2rh + h^2}}{r}\right)\]Using \(r = 6378 \text{ km}\) and \(h = 0.001 \text{ km}\):
\[\Delta c \approx 7.5 \times 10^{-7} \text{ km} = 0.75 \text{ mm}\]