Enter the numbers 1 to 9 into a 3x3 grid such that every row, column and diagonal with 3 cells adds up to 15.
Each number can only be used once.
Up to rotations and reflections, the grid must be filled in like this:
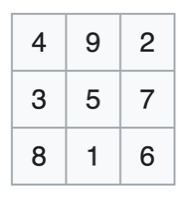
Construction
There are 8 ways to use the numbers 1-9 to add to 15:
- 1+5+9
- 1+6+8
- 2+4+9
- 2+5+8
- 2+6+7
- 3+4+8
- 3+5+7
- 4+5+6
This lines up with the 8 different 3 cell lines we need to fill in, so each sum must be used once. Count the how many times each number appears in a sum - this constraints where it can appear in the grid:
| Number | Count |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 3 |
| 7 | 2 |
| 8 | 4 |
| 9 | 2 |
From this we can tell that:
- 5 is the only number that appears 4 times, so it must be in the center.
- The remaining odd numbers appear 2 times each, so they must be in the middle of the edges. Place 1 and 9 opposite each other, then 3 and 7 in the remaining spots. This is symmetric up to rotations and reflections.
- All the even numbers appear 3 times, so they must be in the corners. Their positions are forced by the numbers that are already filled in. e.g. 2 must be adjacent to the 7 and the 9.