Dominoes
You have a chessboard with two squares removed.

You also have an infinite supply of the dominoes.

Can you cover the entire chessboard with dominoes, with none overlapping, and none going outside the bounds of the board?
It is not possible.
Proof
First colour the chessboard in the normal checkered pattern.

We know that a domino must cover both a black and a white square. However, both the squares missing are black. This means that no matter how you lay the dominoes there will always be two uncovered white squares, which cannot be paired with a black one.
Tetraminos
You have a chessboard with four squares removed.

You also have an infinite supply of the tetraminos.

Can you cover the entire chessboard with tetraminos, with none overlapping, and none going outside the bounds of the board?
It is not possible.
Proof
First colour the chessboard and the tetraminos in the normal checkered pattern.

There are two possible patterns for the tetraminos.
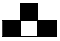
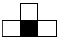
We will put the tetramino such that its colours match with the colour of the squares it is covering. Each of the first kind of tetramino adds three black squares and only one white square. Each of the second kind of tetramino adds three white squares and only one black square.
There’s an equal number of black and white squares, so there must be equally many of both kinds of tetraminos. But there are only \(15 \times 4\) squares left, so there can’t be equal numbers of each kind.